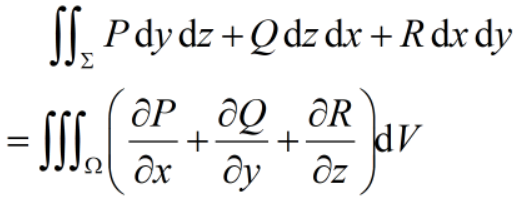百科首页 > 正文

高斯定理（应用于数学等学科的理论）

次浏览 | 更新时间：2023-05-20

来源：网络整理

精选百科

本文由作者推荐

高斯定理

应用于数学等学科的理论

对于一个矢量场V，其散度的体积分等于V在此体积表面上的法向分量的面积分，上述定理被成为高斯定理（英文：Gauss's law），又称为散度定理（Divergence theorem）。

基本信息

中文名

高斯定理

英文名

Gauss's law，Divergence theorem

提出时间

1813年

基本概念

若某封闭区域空间

的边界

由光滑或分片光滑的闭曲面所围成，函数P(x,y,z)，Q(x;y,z)，R(x.y,z)在

上具有一阶连续偏导数，则

式中

是边界曲面

的外侧，称上式为高斯定理，也称为高斯公式或散度定理。此定理揭示了空间区域

上的三重积分与沿

的边界曲面

的面积分之间的关系。

高斯定理能够将计算复杂的曲面积分转化为较为简单的三重积分运算，运用高斯定理还能得出许多有用的推论。

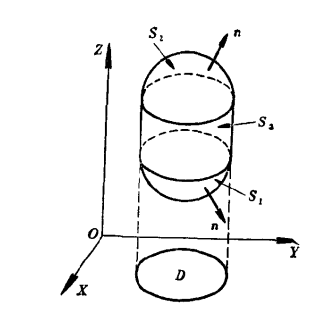
证明

首先假设

是体单连通域，如右图所示构建空间直角坐标系，则

其中

为有界封闭区域，函数

在定义域

上连续，分别记为

，则有

当

为更一般的区域时，可以利用平行于某一坐标平面的平面将该区域分割为若干体单连通域，在这些子区域中均满足上述公式，累加仍可得到上述结果。

同理可证：

将上述三个等式相加，即得到高斯定理。

历史

1826年，苏联数学家奥斯特洛格拉特斯基（Mikhail Ostrogradsky）首先撰文发表了散度定理。由于德国数学家约翰·卡尔·弗里德里希·高斯（Karl Friedrich Gauss）在1813年他的著作中已经研究了这一定理，只是未及时发表，因此散度定理也称为高斯定理。

其他形式

第一类曲面积分形式

由两类曲面之间的联系立即可以给出高斯公式的第一类曲面积分形式：

矢量形式

高斯定理也可以从场论的观点进行阐释。场论是运用数学理论研究某些物理量在空间中的分布状态，如果该物理量为标量，如温度等，则对应的场如温度场等称为标量场。如果该物理量为矢量，如速度等，则对应的场如速度场等称为矢量场。在空间直角坐标系中，一个矢量场

可以表示为：

高斯定理的公式左端可以表示为：

则

称为矢量场A沿闭合曲面

的外侧

穿过的通量。高斯定理的公式左端表示从内穿出的正通量与从外穿入的负通量的代数和，由于指定了

的外侧方向，当

表示该矢量场为净流出，当

表示该矢量场为净流入。

对于上述的矢量场

，其散度可表示为：

与通量类似，散度也是矢量场的一个重要物理量，表示在场中的某一点处通量对体积的变化率。当散度不为0时，称该区域内是有源的，当散度恒为0时，则该区域是无源。

在引入通量和散度的定义后，高斯定理可以表示如下的矢量形式：

从场的观点来看，高斯定理描述了矢量场在某封闭区域中的通量和散度之间的关系，即矢量场

穿出封闭曲面的通量等于

的散度在封闭曲面围成的空间内三重积分。

微分形式

若规定一个作用于

算子

如下：

由散度的定义式可得：

得到结果如下：

上式也称为高斯定理的微分形式。

电磁场中的高斯定理

静电场的高斯定理

静电场中的高斯定理给出了静电场中通过任一闭合曲面的电通量与该闭合曲面内所包围的电荷之间的量值关系，是静电场的一条基本定理。具体来说，在真空中的静电场中，任一闭合面

的电通量

等于该闭合面内的电荷代数和的

分之一，而与闭合面外的电荷无关，公式表示如下：

静电场的高斯定理同样适用于恒定电场中。

磁场的高斯定理

在磁场中，对于任意一个闭合曲面，由于磁感线是闭合曲线，即磁感线进入和传出闭合曲面的数量总是相等的，因此通过任何闭合曲面的总磁通量必为零，称为磁场的高斯定理，也称磁通连续定理，它表明磁场是无源场，用公式表示如下：

磁场的高斯定理也是麦克斯韦方程组的四个方程之一。

高斯定理相关的文章

华山（中国陕西的国家5A级风景名胜区、五岳之一）

华山古称太华山，位于中国陕西省渭南市华阴市城南，为中华五岳之西岳。华山南依秦岭，北临渭水，雄踞关中平原东部，以“奇险天下第一山”闻名于世，也有”华山自古一条路“的说法，景区占地面积约148平方千米。

科威特（君主立宪国）

科威特国（阿拉伯语：دولةالكويت‎，英语：The State of Kuwait），简称科威特（阿拉伯语：الكويت‎），是一个位于西亚地区阿拉伯半岛东北部、波斯湾西北部的君主立宪国。在南部与沙特阿拉伯、北部与伊拉克分别接壤。同伊朗隔海相望，该国首都科威特城与该国名称同名。海岸线长290公

准噶尔盆地（中国第二大的内陆盆地）

准噶尔盆地（英文Junggar Basin；“噶”为gá），位于中国新疆的北部，是中国第二大的内陆盆地。准噶尔盆地位于阿尔泰山与天山之间，西侧为准噶尔西部山地，东至北塔山麓。盆地呈不规则三角形，地势向西倾斜，北部略高于南部，北部的乌伦古湖（布伦托海）湖面高程479.1米，中部的玛纳斯湖湖面270米，

亚历山大大帝（马其顿国王）

亚历山大大帝本词条是多义词，共7个义项马其顿国王西方四大军事统帅之首亚历山大大帝（希腊文：Αλέξανδρος，英文：Alexander the Great；前356年－前323年6月13日），即亚历山大三世，马其顿王国（亚历山大帝国）国王，生于古马其顿王国首都佩拉，马其顿国王腓力二世之子，世界古代史上著名的军事家和政治家。是欧洲历史上最伟大的四大军事统帅之首。曾师从古希腊著名学者亚里士多德，16