精选百科
本文由作者推荐
替代效应
商品价格变化对其需求量的影响
替代效应是指实际收入不变的情况下某种商品价格变化对其需求量的影响。例如，苹果和梨互为替代品。如果苹果的价格上涨，而梨的价格不变，那么相对于苹果而言，梨的价格在下降，消费者就会用梨来代替苹果，从而减少对苹果的需求。这种由于某种商品价格上升而引起的其他商品对这种商品的取代的现象就是替代效应。替代效应使价格上升的商品需求量减少。
基本信息
| 中文名 | 替代效应 |
| 外文名 | substitution effect |
| 结果 | 商品需求量的变化 |
| 学科 | 经济学 |
| 实质 | 价格调节理论 |
| 联系 | 总效应与收入效应、替代效应 |
收起
基本概念
关系
总效应与收入效应、替代效应之间的关系
x商品降价前，x与y两商品的价格比率由预算线aj表示，消费者达到效用最大化的均衡点在E0点，在该点预算线aj与无差异曲线U1相切。与该切点相对应的x商品的购买量为q0，x商品降价后，预算线由aj变为aj2这条新的预算线表示x、y两商品的新的价格比率。新预算线与较高的无差异曲线相切，切点为E2点。E2点是降价后消费者达到效用最大化的均衡点。与该点相对应的x商品的购买量为q2。可见，x商品降价后，其需求量由q0变到q2。
根据这一变化，我们可以用不同条件下该商品需求量的变动，来定义总效应、替代效应与收入效应。
总效应：某商品价格变化的总效应是，当消费者从一个均衡点移动到另一个均衡点时，该商品需求量的总变动。在图-1中，总效应是q2 − q0。
替代效应：替代效应是在商品的相对价格发生变化，而消费者的实际收入不变情况下商品需求量的变化。在图-1中，替代效应是q1 − q0。
这里所说的实际收入不变是指消费者维持在原来的效用水平上，但又要用新的价格比率（由预算线aj2的斜率表示）来度量这一不变的效用水平。降价后，为了使消费者效用水平不变，就必须画一条与预算线aj2，相平行、但是与原无差异曲线U1相切的预算线，在图-1中，这条预算线是a1j1。a1j1与无差异曲线相切于E1点。与E1点相对应的x商品的购买量是q1。
收入效应：一种商品价格变化的收入效应是指在其他所有商品的名义价格与名义收入不变的情况下，完全由实际收入而引起的商品需求量的变化。在图-1中，收入效应是q2 − q1。这纯粹是由实际收入的变化引起的。
总效应与收入效应、替代效应之间的关系是，总效应等于收入效应加替代效应。就图-1而言q2 − q0 = (q1 − q0) + (q2 − q1)。
正常品的收入效应强化了替代效应。一种商品的价格降低，消费者会用该商品去替代其他商品，从而使得该商品需求量增加。但商品价格的下降同时也意味着实际收入的提高，对正常品而言，这就意味着需求量的增加。由于收入效应与替代效应在同一方向上起作用。所以，对正常品而言，其需求量与价格反方向变化。
正常品收入效应与替代效应同方向变化的情况由图-1中的箭头来表示。
劣等品的收入效应与替代效应
劣等品的情况不同于正常品。由于劣等品的需求收入弹性小于零，因而劣等品的收入效应是需求量与实际收入反方向变化，即实际收入增加，需求量减少；实际收入减少，需求量增加。
替代效应
收入效应=(q2 − q0) − (q1 − q0) = q2 − q1
图-2表明q2小于q1，所以收入效应是负的值，说明收入替代效应在相反的方向起作用价格消费线（如图-2中的箭头方向所示），收入效应小于零的结果是使得总效应小于替代效应。
尽管收入效应与替代效应在相反的方向起作用，由于在绝对值上替代效应大于收入效应，所以价格下降总的结果是该商品的需求量增加了。价格消费线仍向右方倾斜。由此而导出的需求曲线也是向右下方倾斜的。因此，即使是劣等品，一般情况下也遵循需求法则，只不过需求曲线的价格弹性比较小。
需求曲线
一种商品价格下降是否导致消费者选择该商品数量的增加，取决于价格下降产生的替代效应和收入效应的符号和大小。正常商品和低档商品的替代效应和收入效应对正常商品而言，商品价格下降的替代效应和收入效应都使得该商品需求量增加；对于低档商品而言，价格下降的替代效应使商品需求量增加，但收入效应却使得商品需求量下降。
替代效应和收入效应与消费者需求曲线利用替代效应和收入效应说明消费者需求曲线的形状一种商品价格上升是否导致消费者选择该商品数量的增加，取决于价格下降产生的替代效应和收入效应的符号和大小。
正常商品
替代效应
正常商品的替代效应为正******(替代效应总是负值：甲商品价格上涨，乙商品需求量增加——负效应；方向相反为负值），收入效应也为正。
低档商品
替代效应
总之，低档物品的替代效应与价格成反方向的变动，收入效应与价格成同方向的变动，而且，在大多数的场合，收入效应的作用小于替代效应的作用，所以，总效应与价格成反方向的变动，相应的需求曲线是向右下方倾斜的。（但也会出现收入效应大于替代效应的情况，就是吉芬物品。
吉芬商品
如果为负的收入效应的绝对值大于替代效应，使得需求量随价格上升而上升，则该商品为吉芬商品。吉芬商品价格变动的替代效应和收入效应吉芬商品价格变动的替代效应为正，收入效应为负（更大），并且收入效应大于替代效应，使得需求量随价格上升而上升。
若收入效应与替代效应在相反的方向起作用，而且从绝对值上讲收入效应大于替代效应，则该商品是一种特殊的劣等品，称为吉芬商品。
图-3显示了吉芬商品的收入效应与替代效应。图中，总效应为q2 − q0，由于q2小于q0，所以x商品降价后的总效应是负的值；替代效应为q1 − q0；收入效应为(q2 − q0) − (q1 − q0) = q2 − q1
替代效应
可以就商品降价后所产生的各种效应的变化归结如下。不管商品是正常品，还是一般的劣等品，或是吉芬商品，商品降价后的替代效应总是正值，这表明，只要该商品降价，消费者就会用该商品去替代其他商品。对于正常品而言，收入效应与替代效应在同一方向上起作用，表明在商品降价后，收入效应与替代效应都是正值。总效应必然大于零，表示商品降价后需求量增加。对于一般的劣等品而言，虽然收入效应与替代效应在相反的方向起作用，但是在绝对值上替代效应仍然大于收入效应。商品降价后正值的替代效应在绝对值上大于负值的收入效应，总效应仍然大于零，表示商品降价后需求量也是增加的。只有那些特殊劣等品即吉芬商品，在商品降价后，不仅收入效应与替代效应在相反的方向起作用，而且在绝对值上收入效应大于替代效应，导致商品降价后总效应小于零。这表明商品降价后，需求量不仅没有增加，反而减少了。
希克斯
来源
希克斯替代效应（Hicksian substitution effect）与斯勒茨基替代效应（Slutsky substitution effect）是分别以两位经济学家约翰·希克斯（John Richard Hicks，1904年4月8日—1989年5月20日）与斯勒茨基（E. Slustsky）的名字命名的。
含义
替代效应是指消费者实际收入不变时，某种商品价格变化使得消费者选择该种商品的替代品，造成对该商品需求量的影响。
斯勒茨基分解下的，替代效应：
1、完全互补情况下，替代效应为零，总效应为收入效应。
2、完全替代情况下，总效应为替代效应，收入效应为零。
对比
如前所述，替代效应是指商品相对价格变化后，而令消费者实际收入不变情况下所引起的商品需求量的变化。希克斯替代效应与斯勒茨基替代效应的差别，在于他们对什么是消费者实际收入不变所下的不同定义。在希克斯替代效应中，实际收入不变是指使消费者在价格变化前后保持在同一条无差异曲线上；而在斯勒茨基替代效应中，实际收入不变是指消费者在价格变化后能够买到价格变动以前的商品组合。
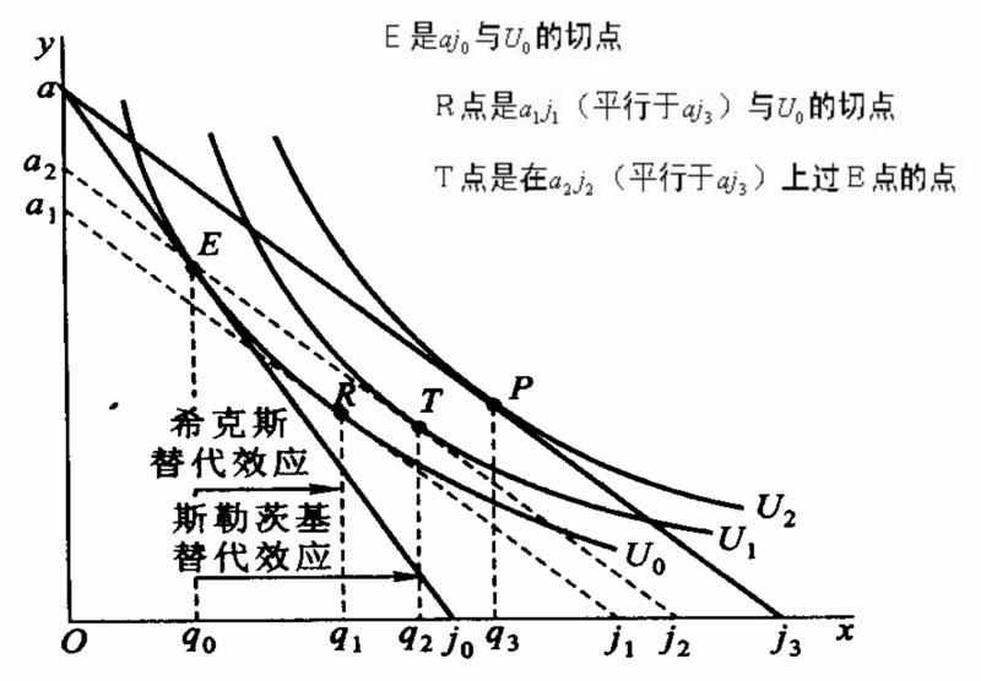
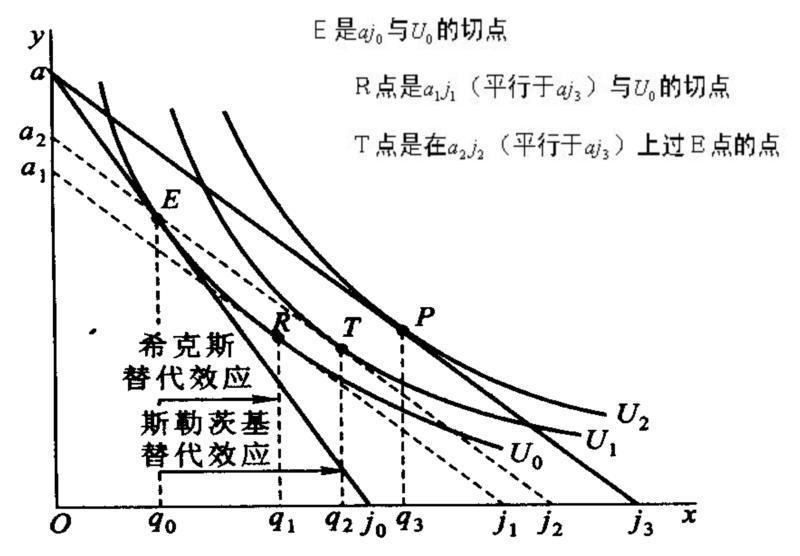
图-4 希克斯替代效应与斯勒茨基替代效应
替代效应
图-4中的横坐标表示某种特定的商品，纵坐标y表示除了x商品以外的所有其他商品。我们讨论y商品价格不变，x商品价格下降以后的斯勒茨基替代效应。x商品降价前，预算线为aj0，aj0与无差异曲线U0相切于E点，E点是消费者效用最大化的均衡点。在E点，x商品的购买量为q0。x商品降价后，预算线变为aj3，消费者效用最大化的均衡点为P点。
假定我们想在x商品降价后维持消费者的实际收入不变。按照希克斯替代效应中所定义的实际收入，应该使消费者在新的价格比率下回到x商品降价前的无差异曲线上，通过画一条与aj3相平行、并与原无差异曲线U0相切的预算线可以保证这种意义上的实际收入不变。图-4中a1j1线便是我们所需要的预算线，a1j1与U0相切于R点，与R点相对应的x商品的购买量为q1，q1 − q0便是希克斯替代效应。
按照斯勒茨基替代效应中所定义的实际收入，若想在x商品降价后维持消费者的实际收入不变，应该使消费者在新的价格比率下能够购买他在降价前所能购买的商品数量，即能够购买图-4中E点所表示的商品数量。通过画一条与预算线aj3相平行、并且过E点的预算线可以保证这种意义上的实际收入不变。图-4中的a2j2线便是我们所需要的预算线。a2j2和一条高于无差异曲线U0、低于无差异曲线U2的无差异曲线U1相切，切点为T。与T点相对应的x商品的购买量为q2。q2 − q0为斯勒茨基替代效应。由于q2大于q1，所以斯勒茨基替代效应大于希克斯替代效应。
x = x(Px,M)（3.35）
降价后对x商品的需求函数为
x`=x(P`x,M`) (3.36）
x商品降价后对x商品需求的总效应为
Δx =x(P`x,M)-x(Px,M) （3.37）
分为两部分，收入效应Δxm与替代效应Δx5，
Δx = Δxm + Δx5（3.38）
Δx5=x(P`x,M)-x(Px,M) （3.39）
其中是在x降价为后，为了维持降价前的购买数量组合而调整后的收入。
Δxm=x(P`x,M)-x(P`x,M`) （3.40）
因此， Δx =Δxm+Δx5=[x(P`x,M`)-x(Px,M)]+[x(P`x,M)-x(P`x,M`) ]（3.41）
（3.41）式与（3.37）式虽然是恒等式，但（3.41）式是以代数形式将商品价格变化后的收入效应与替代效应明确地表示出来。
由Δx = Δxm + Δx5，我们知道，x商品价格变动后总效应Δx符号取正的值还是取负的值，取决于x商品是工常品、一般劣等品、还是吉芬商品。我们分x商品降价与提价两种情况进行讨论。
若x商品降价，Δx5总是取正的值。对于正常品而言，Δxm也取正的值，因此总效应Δx的值是正的；对于一般劣等品而言，降价后，Δxm取负的值，但从绝对值讲，Δxm小于Δx5，因此总效应Δx的值仍然是正的；对于吉芬商品而言，降价后，Δxm取负的值，而且从绝对值讲，Δxm大于Δx5，因此总效应Δx的值是负的。
若x商品提价，Δx5总是取负的值。对于正常品而言，Δxm也取负的值，因此总效应Δx的值是负的；对于一般劣等品而言，提价后，Δxm取正的值，但从绝对值讲，小于Δx5，因此总效应Δx的值仍然是负的；对于吉芬商品而言，提价后，取正的值，而且从绝对值讲，Δxm大于Δx5，因此总效应Δx的值是正的。
在x商品价格变动后，要维持消技者的实际收入不变，即要使消费者能够买得起x商品价格变动前他所购买的各种商品组合量，收入应该变动多大的数量？也就是说，当x商品的价格变动为ΔPx时，ΔM是多少？可以证明
ΔM=ΔPx·x（3.42）
（3.42）式的推导过程如下。假定消费者消费x、y（y代表除x商品以外的所有其他商品）两种商品。x商品价格变动前，消费者的预算线为
M=ΔPx·x+Py·y（3.43）
x商品价格由Px变为P`x后，要便消费者仍能购买他在价格变动前所能购买的x、y数量，预算线应该是
M`=P`x·x+Py·y（3.44）
我们已经指出，M'是x商品价格变动后，为了维持价格变动前的购买数量组合而调整后的收入。由（3.43）式与（3.44）式我们得到
这便是（3.42）式。
参考
斯勒茨基替代效应的概念可以作为政府制定政策的参考。例如，政府决定在猪肉涨价后对消费者进行价格补贴。假定消费者每月消费2.5千克肉，原价12元钱1千克肉。现价格提高到14元钱1千克，要使消费者在肉涨价后仍能买得起2.5千克肉，给消费者的补贴应该是
ΔM=ΔPx·x=(P`x-Px)·x=(14.00-12.00)*2.5=5(元)。
商品价格变化所引起的替代效应与收入效应
商品类别 替代效应与价格的关系收入效应与价格的关系 总效应与价格的关系需求曲线的形状
正常品 反方向变化 反方向变化 反方向变化 向右下方倾斜
低档品 反方向变化 同方向变化 反方向变化 向右下方倾斜
吉芬商品反方向变化 同方向变化 同方向变化 向右上方倾斜
替代效应相关的文章
风热，是病证名，风和热相结合的病邪，临床表现为发热重、恶寒较轻、咳嗽、口渴、舌边尖红、苔微黄、脉浮数，甚则口燥、目赤、咽痛、衄血等。是风热之邪犯表、肺气失和所致。治以疏风清热为主。
尼摩星，《神雕侠侣》中的人物，蒙古三杰之一，来自天竺国的高手，擅长瑜珈之术，武功狠辣高强，使用一条蛇形铁鞭，因名利所惑效力于忽必烈。生性勇悍自负，虽非光有武力之辈，却沉不住气立功心切，受金轮法王诱骗，误中冰魄银针毒，被迫自断双腿，保住性命。后来，尼摩星在羊太傅庙中袭击郭芙、郭襄姐妹，几近成功之际，却
小编整理：玉蜂是一种出自金庸先生的原著《神雕侠侣》中的虚构昆虫。小龙女是古墓派第三代掌门人，金庸笔下广受读者喜爱的女主角之一。擅驭蜂，喜音律，精琴艺缝纫，悟禅道，她将音乐融于武功之中，可用琴音与人交流。，小龙女在小说中曾用玉蜂针伤了金轮国师。玉蜂《神雕侠侣》中
阿卜杜拉·阿齐兹·伊本·沙特是阿卜杜·拉赫曼的儿子，出生于1880年，从小在科威特长大。1902年在科威特酋长穆巴拉克·萨巴赫的支持下，21岁的阿齐兹带领40多个勇士，骑着骆驼，向利雅得发起进攻，夺回利雅得，建立第三个沙特酋长国。
伊玛目清真寺又称“马斯吉迪·贾米伊·阿巴斯”或“国王清真寺”，位于伊朗伊斯法罕。清真寺里外均由精美的瓷砖镶嵌而成，其外形为壁竞式的正门面向正北。清真寺的大门是镀银的，正门高达30米，门上写有许多诗文，由当时著名书法家用美丽的波斯文纳斯塔利克体书写。
尚可名片
这家伙太懒了，什么都没写！
作者
