百科首页 > 正文

屈光度（屈光力的大小单位）

次浏览 | 更新时间：2023-05-22

来源：网络整理

精选百科

本文由作者推荐

屈光度

屈光力的大小单位

屈光度是屈光力的大小单位，以D表示，即指平行光线经过该屈光物质，以焦点在1m时该屈光物质的屈光力为1屈光度或1D。

以透镜而言，是指透镜焦度的单位如一透镜的焦距1m时，则此镜片的屈折力为1D屈光度与焦距或反应。

基本信息

中文名	屈光度
外文名	Dioptre（英），Diopter（美）
属性	物理学
大小单位	屈光力
单位	D

简介

屈光度

光线由一种物体射入到另一种光密度不同的物质时，其光线的传播方向产生偏折，这种现象称为屈光现象，表示这种屈光现象大小（屈光力）的单位是屈光度（缩写为“D”）。1D屈光力相当于可将平行光线聚焦在1米焦距上。

眼睛折射光线的作用叫屈光，用光焦度来表示屈光的能力，叫做屈光度。眼睛不使用调节时的屈光状态，称为静态屈光，标准眼静态屈光的光焦度+58.64D。人眼在使用调节时的屈光状态，称为动态屈光，其光焦度强于静态屈光的光焦度。由于眼睛屈光度不正确，造成不能准确在视网膜成像，就是视力缺陷，一般情况需要佩带眼镜，通过镜片补充和矫正眼睛本身的屈光度，达到视网膜正确成像的目的！

屈光度，或称焦度，英语用“Dioptre”表示，是量度透镜屈光能力的单位。

焦距f的长短标志着折光能力的大小，焦距越短，其折光能力就越大，近视的原因就是眼睛折光能力太大，远视的人则折光能力太弱。

焦距的倒数叫做透镜焦度，或屈光度，用φ表示。如果焦距是10cm，那么φ=10D。

凸透镜（如：远视镜片）的度数是正数(+)，凹透镜（如：近视镜片）的度数是负数(-)。

一个+3屈光度的透镜，会把平行的光线聚焦在镜片的1/3米外。

屈光度的单位简写是D，国际单位制的单位是 m的-1次方。

一般眼镜常使用度数来表示屈光度，以屈光度 D 的数值乘以 100 就是度数[1] ，例如 -1.0D 等于近视眼镜（凹透镜）的 100度。

检查

屈光度

主要方法有以下几种：

视网膜检影镜法

这是一种客观检查法。检查者手持视网膜镜（中央有孔的小圆反光镜），离开眼球1米远，将光线反射到眼球里。光线通过屈光间质到达视网膜，视网膜将光线原路反射出眼球。检查者通过视网膜镜中央的小圆孔，可以看到反射回来的光线。由于屈光间质的屈光能力不同，反射光的影像表现不同。影像与视网膜镜的移动方向一致，称为顺动，反之称为逆动。远视眼反射光的影像顺动，近视眼反射光的影像逆动。检查者为了使影像不动，需要不断在受检者的眼前加不同的眼镜片，加到影像静止为止，说明镜片已经中和了眼球的屈光不正。换句话说，镜片的屈光度就是眼球屈光不正的度数。

自动验光仪验光法

用自动检查仪代替检查者手里拿的视网膜镜和各种镜片。

计算

屈光力越强，焦距越短。2D屈光力的透镜焦距为1/2m或50cm。如果想知道透镜的焦距，用100cm，也就是1.00m除以屈光力，结果即为焦距。例如，5D屈光力的焦距为20cm。（100cm除以5D=20cm。）凸透镜的屈光力以“+”号表示，凹透镜的屈光力以“—”表示。 1 屈光度或 1D 等于常说的 100 度。

眼镜的度数=屈光度数×100

调节

在一些光学仪器上比如相机、望远镜、显微镜等器材上，都考虑到了使用者在不方便佩带眼镜观看时各人

相机的屈光度调节装置

眼睛的视力差异，所以都具有屈光度调节装置。因此，“屈光度”这个概念是眼镜的，如200度的近视镜屈光度为-2D，150度的老花镜的屈光度为+1.5D。KWP海岸线网络安全资讯站一些高档相机为了方便一些轻微近视或老花的人群不戴眼镜可以直接观看取景器内的效果增加了屈光度调节装置。屈光度调节装置其实就是在相机取景目镜处加一组镜片，通过旋钮等调整镜片位置关系，使其达到一定范围内的连续屈光度转换。范围一般在-3D到+2D之间。由于屈光度调节范围是有限的，超过这个范围的中度近视等用户可以另外选购专用的目镜调节镜。专为近视用户开发的目镜调节镜，屈光度分别为-1、-2、-3、-4等；专为远视用户开发的目镜调节镜，屈光度分别为+0.5、+1、+1.5、+2、+3等。用户可根据自己的视力情况，选择合适的目镜校正镜加装在目镜内，可以裸视进行拍摄。屈光度调节功能不仅在单反相机，并增加部分成本等原因，对于最重视小巧便携的卡片式数码相机一般都没有。屈光度可调眼镜根据现有通用矫正视力缺陷（近、远视眼）眼镜的镜片形状固定，屈光度不能调节的缺点，本实用新型将镜片分为镜片和透镜两部分；透镜又由锅底形里层、外层和液层三层构成。锅底形里层的周边，有一向外转折且与外层相连的透镜边，形成周边封闭的层状液体容纳空间。镜片外侧的镜片边上开有通液孔道，其一端开口于液层，一端与设置在镜片外侧的镜片边内的液压调节装置相连。当启动液压调节装置，使液层的液体压力渐渐加大时，则凹透镜的屈光度由大渐小，而凸透镜的屈光度则由小渐大；反之，凹透镜的屈光度由小渐大，而凸透镜的屈光度则由大渐小，由此实现眼镜屈光度的自由调节。?

作用

第一点

对于同种材料制成的凸透镜，其凸度越大，屈光度数越大，反之越小。换言之，对同一只眼球而言，近视度

眼镜度数检测

数越高，眼球越突出，需戴近视镜度数越高。

第二点

眼球的屈光系统是个可调的“凸透镜”，因而形态可变，当眼前放上凹透镜时，眼球仍具有自我调节功能，眼睛能看清不同距离的目标和近视或老视患者戴镜能适应本身就说明了这一点。

第三点

由于普通眼镜与眼球相分离，形象直观，容易计算。本节探讨的重点是眼镜对眼球屈光的影响，对有关眼镜的论述，都是针对普通眼镜。戴角膜接触镜与普通眼镜在屈光方面具有相同的效果，其原理和技术在眼镜行业已经很成熟，因此不再论述。

第四点

在屈光学中，只有在某些特殊情况下，屈光度数为P1、P2两透镜组合产生的屈光效果才是屈光度为P1+P2的透镜。在眼球与透镜组成的光路中，在效果上或定性的计算中，也可以有P1+P2这种情况，这并非透镜组合后的实际屈光效果，而是一种简化和近似，因为眼睛具有自我改变屈光度的能力。虽然较难用实验验证，但从眼球的调节效果看，它应当具有抵消镜片屈光度的作用，而该公式却具有简化计算的作用。对于眼球和透镜所组成的系统来说，至多是两个透镜组成的屈光系统，因此可以利用屈光学理论进行计算。当戴上透镜时，因眼球特殊的调节作用，将透镜的屈光度和眼球调节适应后的屈光度相加减，也可得到近似值，虽然与准确地测量眼球的屈光力尚有一段距离，但在效果上却接近。在该论证中，尽管从理论上进行了推导，但实验和测量都非常困难，就象配制近视镜需要试戴一样，在用来指导配镜的过程中还要进行试验。

第五点

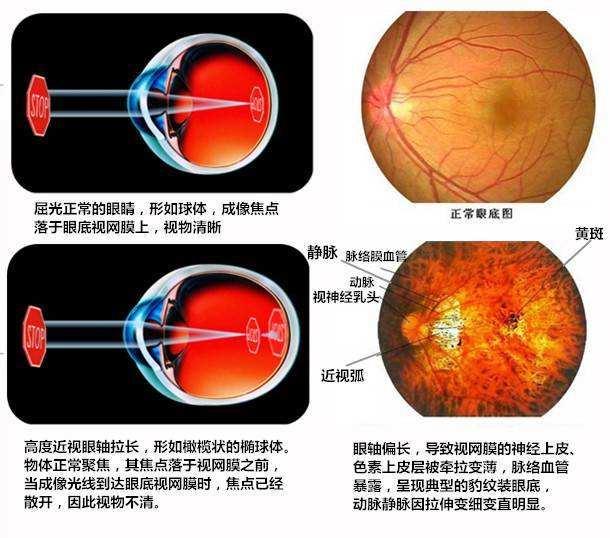
从眼球的屈光特点看，有人测得眼球的静屈光力为+58.6D,这虽然是一特例，但也基本反映出眼球具有很强

的屈光力，其调节相对较小，正常眼为0——10D左右，近视眼为n——10D(n指眼球的近视屈光度数)左右，而它又固定在眼眶内，因此对某一个人来说，可以认为眼球的屈光系统——“透镜”的中心到视网膜的距离不变，在以后的计算中，可认为像距为常数K，对于眼球的屈光来说，如果能在视网膜上成清晰的像，该屈光系统仍满足透镜成像公式

1/u+1/k=P

其中K是常数，P为眼球的屈光度数，是变量，意思是不同的人看不同距离的目标和不同的人眼球的屈光度数不同，U指目标到眼球的距离。该公式成立的条件是：某一时刻，眼睛看某一距离的目标，且目标在眼睛的近、远点之间。从公式看，正视眼看无穷远处时1/u=0，上式可化为P=1/K，可令1/k=P0,即P0为眼球的静屈光度。当看距眼球为L的目标时，“透镜”成像公式变为1/L+1/K=1/L+P0,1/L为眼球增加的屈光度数，1/L+P0即为眼球看距离为L的目标时的屈光度。

对于戴镜者来说，在一般情况下，眼球到眼镜中心的距离约为1.2——2.4CM,以下用h表示，但对于某人某一时刻的值是确定的，设屈光度为P'的透镜的焦距为F，当看距离为L的目标时，镜片成像公式如下:

1/L+1/V=P'==>1/V=P'-1/L①

此时透镜所成像到眼球这一“透镜”的距离为|V|+h,眼球的屈光情况满足公式:1/(|V|+h)+1/K=P②

从公式看，如果|V|比h大得多，根据①公式，②式可近似简化为:

1/|V|+1/K=D=|D'-1/L|+1/K③

由于眼睛透过透镜看到的是虚像，V<0,则1/|V|+1/K=1/L+1/K-D'=D1+D0-D'

近视眼镜

计算，在看距离不太近、镜片度数不太高的目标时，可忽略h，这样可简化计算，有利于定性分析。换言之，对于薄透镜来说，如果忽略眼球到镜片的距离，可以认为因戴近视眼镜致使眼球调节增加的调节度数等于透镜的屈光度数。在眼球与眼镜组成的光学系统中，各部分所产生的屈光度数可近似相加减，这种分析可使计算简化，使问题变得容易。在以后的论述中，我们将利用这一结果进行定性分析和近似计算。

第六点

误差分析。如果以公式为标准，那么产生误差的原因是多方面的，现对此分析。

(1)因为眼球的调节与形变同时进行，有调节就有形变，有形变就有眼球前后径的变化，还由于晶状体和角膜本身形变而导致的角膜、房水、晶状体所组成的“凸透镜”光心的变化。虽然近视或老视本身并不能说明其前后径的变化(一说，近视眼是眼球成像在视网膜前方，但近调节的过强或睫状肌不能放松都可实现这一点，不能充分说明眼球前后径变长)，但更不能说明其不变性。这些因素的存在决定了公式中K只是一个近似，而且近调节幅度越大，K值变化越大，这是产生误差的一个原因。但考虑到在眼球调节中，晶状体的屈光度调节和眼球的屈光度(约60屈光度)相差很远，而眼球调节幅度一般少于10个屈光度，相对较小，角膜屈光度变化更小，因此，可认为“透镜”光心到视网膜的距离几乎不变。

(2)因每个人的眼球前后径不等，对不同的人而言，K并非常数，很难准确测量，但具体到某一个人的某一阶段而言，眼球前后径不变，可认为K是常数。

(3)对不同的人而言，眼镜片到“凸透镜”光学中心的距离是一较难测量的变量，这也影响到计算的准确性。由计算可知，h增大时，误差增大，反之越小。

第七点

在眼前放置透镜时，与正常眼相比，如果眼睛仍然能看清目标，从眼球的调节效果看，眼镜首先抵消眼球调节的不足，因此在以后的计算中，只要在眼球正常的调节范围内，用于抵消透镜的效果在理论上能够成立，我们无须注意眼球实际屈光度的变化。对眼球来说，不管戴多少屈光度的眼镜，要看清前面的目标，必须低消眼镜的作用而增加屈光度调节。

第八点

由于配镜误差、适应等原因，即使把各种因素都考虑进去，理论对于实践也只是一种近似，眼球调节幅度较大时，这种简单化、理想化的理论会因自身形变而使误差增大。再者，镜片到眼球光学中心的距离随不同的人而不同，这又无法用物理公式表示，在具体配制时要具体问题具体分析。

第九点

对于眼球和镜片所组成的屈光系统来说，镜片度数是确定的，而眼球的屈光度数却是个变量，因此，把眼球看成是一个可调凸透镜的意思是：眼睛透过眼镜能看清某一目标时，眼球的屈光度数确定，因而完全可以利用屈光学理论进行计算，但眼球看目标的距离发生变化时，其屈光度数也随之变化。

第十点

对眼球与眼镜组成的屈光系统而言，只有两个“透镜”组成，可看成一个等效的透镜组，透镜的度数可相加减，比如一个+5D的透镜，可看成是一个(+2D)+(+3D)的透镜组，虽然在多数情况下并不成立，但在理论为我们解决问题提供了方便。

参考资料

[1]

资料来源[引用日期2019-07-29]

屈光度相关的文章

植物界（生物的一界）

植物界（学名：plant kingdom）为生物的一界。在不同的生物分界系统中，植物的概念及其所包括的类群也不一样，如将生物分为植物和动物两界时，植物界包括藻类、菌类、地衣、苔藓、蕨类和种子植物；在五界的系统中，植物界仅包括多细胞的光合自养的类群，而菌类、地衣和单细胞藻类以及原核的蓝藻则不包括在内。

野菊（菊属多年生草本植物）

野菊（学名：Chrysanthemum indicum Linnaeus），又名山菊花、黄菊仔、菊花脑、疟疾草，是菊科（Asteraceae）菊属(Chrysanthemum)一种多年生草本植物。野菊分布较为广泛，主要分布在印度、日本、朝鲜、韩国、中国，在中国主要分布在东北、华北、华中、华南及西南各