小编整理:
杠杆原理也称为“杠杆平衡条件”,是分析杠杆受力平衡的定理,最早由古希腊科学家阿基米德提出。杠杆要达到受力平衡,作用在杠杆上的两个力矩(力与力臂的乘积)必须大小相等,旋转方向相反。也就是说,杠杆的平衡条件必须满足:动力×动力臂必须等于阻力×阻力臂,数学表达式为:F×L点评一下:杠杆原理(杠杆受力平衡原理)杠杆原理也称为“杠杆平衡条件”,是分析杠杆受力平衡的定理,最早由古希腊科学家阿基米德提出。杠杆要达到受力平衡,作用在杠杆上的两个力矩(力与力臂的乘积)必须大小相等,旋转方向相反。也就是说,杠杆的平衡条件必须满足:动力×动力臂必须等于阻力×阻力臂,数学表达式为:F1·L1=F2·L2。式中,F1表示动力,L1表示动力臂,F2表示阻力,L2表示阻力臂。 | 中文名 | 杠杆原理 |
| 外文名 | lever principle |
| 表达式 | F1·L1=F2·L2 |
| 应用学科 | |
| 提出时间 | 公元前三世纪 |
| 提出者 | 阿基米德、墨子 |
| 适用领域 | 杠杆力学 |
| 别名 | 杠杆平衡条件 |
收起
古希腊科学家阿基米德最早在《论平面图形的平衡》一书中提出了杠杆原理。他曾有一句广为流传的名言:“给我一个支点,我就能撬起整个地球!”,这句话说的便是杠杆原理。
在杠杆原理提出之前,阿基米德先把杠杆实际中的一些经验知识当作“不证自明的公理”,这些公理包括
1)在无重量的杆的两端离支点相等的距离处挂上相等的重量,它们将平衡;
2)在无重量的杆的两端离支点相等的距离处挂上不相等的重量,重的一端将下倾;
3)在无重量的杆的两端离支点不相等距离处挂上相等重量,距离远的一端将下 倾;
4)一个重物的作用可以用几个均匀分布的重物的作用来代替,只要重心的位置保持不变。相反,几个均匀分布的重物可以用一个悬挂在它们的重心处的重物来代替
然后,基于这些公理,他运用严谨的几何学及逻辑论,提出了杠杆原理。阿基米德认为,二重物平衡时,它们离支点的距离与重量成反比。
阿基米德除了对杠杆进行研究理论外,还将该原理付诸于实践。据说,他曾借助杠杆和滑轮组,使停放在沙滩上的船只顺利下水;在保卫叙拉古免受罗马海军袭击的战斗中,他利用杠杆原理制造了远、近距离的投石器,发射出各种飞弹和巨石攻击敌人,曾把罗马人阻于叙拉古城外达3年之久。 中国战国时期的墨子也曾对杠杆进行过探究。据《墨子 · 经说下》记载:“衡,加重于其一旁,必捶,权重相若也。相衡,则本短标长。两加焉重相若,则标必下,标得权也”。这两条对杠杆的平衡说得很全面。里面有等臂的,有不等臂的;有改变两端重量使它偏动的,也有改变两臂长度使它偏动的。 使用杠杆时,为了省力,就应该用动力臂比阻力臂长的杠杆;如果想要省距离,就应该用动力臂比阻力臂短的杠杆。因此使用杠杆可以省力,也可以省距离。但是,要想省力,就必须多移动距离;要想少移动距离,就必须多费些力。要想又省力而又少移动距离,是不可能实现的。
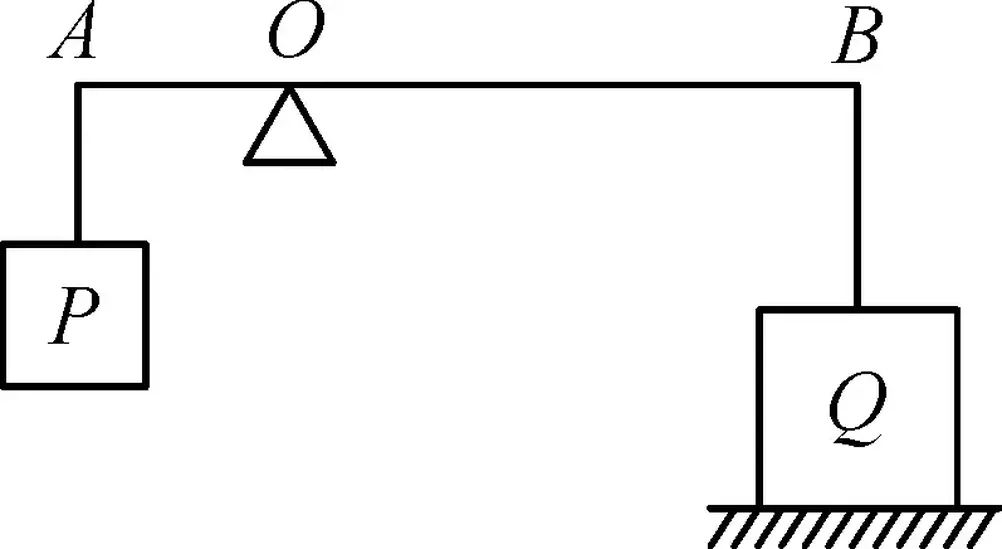
杠杆的支点不一定要在中间,满足以下三个点的系统,基本上就是杠杆:支点、施力点、受力点。
动力臂延伸
杠杆有省力杠杆,也有费力杠杆,两者功能表现有所不同。例如脚踩的打气机,手压的榨汁机,就是省力杠杆 (动力臂 > 阻力臂);尽管省力了,但我们却要压下较大的距离,受力端只有较小的动作。另有一种是费力杠杆。例如路边的吊车,钓东西的钩子在整个杆的尖端,尾端是支点、中间是油压机 (力矩 > 力臂),这就是费力的杠杆。但费力换来的是中间的施力点只要动小距离,尖端的挂勾就会移动相当大的距离。 两种杠杆都有用处,不同的应用场景需要评估是要省力或是省下动作范围。另外,有种机械叫轮轴,也可当作是一种杠杆的应用,只是表现上有时需要增加转动的计算。
阿基米德的名言:"假如给我一个支点,就能撬起地球!"不仅催人奋进,更有着严谨的科学根据。
杠杆平衡是指杠杆在动力和阻力作用下处于静止状态下或者匀速转动的状态下。杠杆受力通常有两种情况。
1)杠杆上受两个力作用时
动力×支点到动力作用线的距离=阻力×支点到阻力作用线的距离,即动力×动力臂=阻力×阻力臂,代数式表示为F1×L1=F2×L2 2)杠杆上受多个力作用时
所有使杠杆顺时针转动的力的大小与其对应力臂的乘积等于使杠杆逆时针转动的力的大小与其对应力臂的乘积。这也叫作杠杆的顺逆原则,同样适用于只受两个力作用的情况。
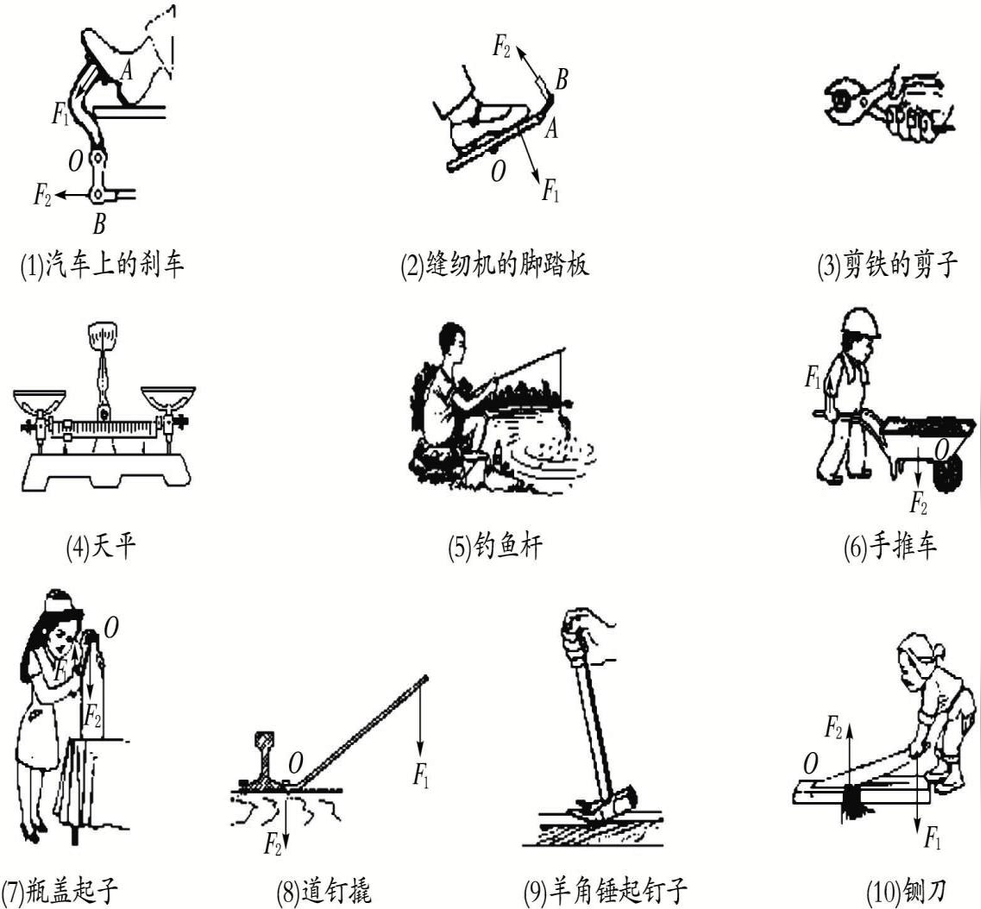
杠杆的分类
省力杠杆
L1>L2,F1
费力杠杆
L1F2,费力、省距离。
如钓鱼竿、镊子,筷子,船桨裁缝用的剪刀 理发师用的剪刀等。 等臂杠杆
L1=L2,F1=F2,既不省力也不费力,又不多移动距离,
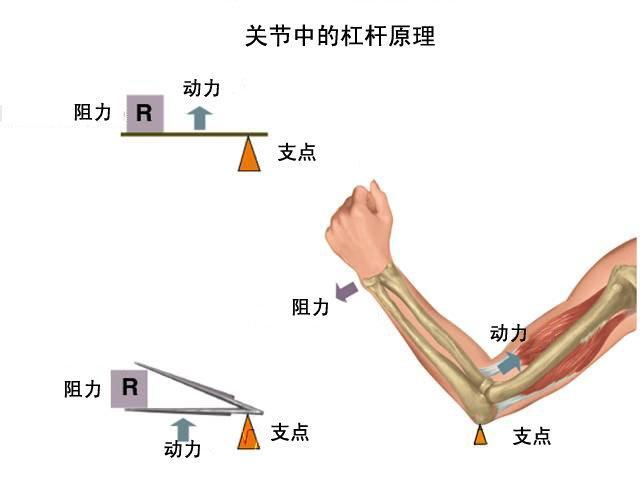
费力杠杆
人体中大部分杠杆为费力杠杆,也有小部分是等臂和省力杠杆。
点一下头或抬一下头是靠杠杆的作用,杠杆的支点在脊柱之顶,支点前后各有肌肉,头颅的重量是阻力。支点前后的肌肉配合起来,有的收缩有的拉长配合起来形成低头仰头。
当曲肘把重物举起来的时候,手臂也是一个杠杆。肘关节是支点,支点左右都有肌肉。这是一种费力杠杆,举起一份的重量,肌肉要花费6倍以上的力气,虽然费力,但是可以省一定距离。 当你把脚尖翘起来的时候,是脚跟后面的肌肉在起作用,脚尖是支点,体重落在两者之间。这是一个省力杠杆,肌肉的拉力比体重要小。而且脚越长越省力。
如果你弯一下腰,肌肉就要付出接近1200牛顿的力量。这是 由于在腰部肌肉和脊骨之间形成的杠杆也是一个费力杠杆。所以在弯腰提起立物时,正确的姿式是尽量使重物离身体近一些,以避免肌肉被拉伤。
在简单的二元系相图中。恒温连接线和液相线固相线有两个焦点。处在连接线上任一点所代表的体系状态都会发生两相平衡。体系成分固定后,AB两项成分分别是xbA和xbB。 根据质量守恒。该温度平衡的AB两项的相对量。
AA(wA)=(xbB-xb)/(xbB-xbA)
AB(wB)=(xb-xbB)/(xbB-xbA)
注意:杠杆定律是由于质量守恒推导出来的,不一定平衡才满足。无论系统是否平衡都应该满足杠杆原理。 举起地球
阿基米德将自己锁在一间小屋里,夜以继日地埋头写作《浮体论》。这天,一位朝臣突然闯进来,一进门就喊道:“原来您躲在这里。国王正调动人马四处找你呢。阿基米德心想:外面一定出大事了。他立即收拾起书稿,随大臣一同出去,直奔王宫。
当他们来到宫殿前,看见卫兵们银枪铁盔,殿内文武满座,国王正焦急地在地毯上来回踱步,宫殿内的长条案上摆着海防图、陆防图。阿基米德知道,他最担心的战争终于爆发了。 原来地中海沿岸的罗马王朝和迦太基连年征战,双方互有胜负。叙拉古是夹在迦、罗两个强国中的城邦小国,常常随着两个强国的胜负而弃弱附强,飘忽不定。阿基米德对这种外交策略很不放心,曾多次告诫国王,不要惹祸上身。可是叙拉古的国王年少无知,刚愎自用,惹恼了罗马人。现在打了胜仗的罗马人决定从海陆两路进攻叙拉古,国王吓得没了主意。当他看到阿基米德来了,连忙恳求道:“亲爱的阿基米德,你是最聪明的人,先王在世时说过你都能推动地球。” 关于阿基米德推动地球的说法,要追溯到他在亚历山大里亚留学。当时,他从埃及农民提水用的吊杆和奴隶们撬石头用的撬棍受到启发,发现可以借助杠杆来达到省力的目的,而且发现,手握的地方到支点的这一段距离越长,就越省力气。由此他提出了这样一个定理:力臂和力(重量)的关系成反比例。这就是杠杆原理。用现在的表达方式表述就是:动力×动力臂=阻力×阻力臂。为此,他曾给当时的国王亥尼洛写信说: `我不费吹灰之力,就可以随便移动任何重量的东西;只要给我一个支点,给我一根足够长的杠杆,我连地球都可以推动。' 可现在的国王并不懂得什么叫科学,他只知道大难临头了,希望阿基米德能够救驾。 可是罗马军队实在太厉害了,四个罗马陆军军团已经挺进到了叙拉古城的西北,城外鼓声齐鸣,杀声震天。危急关头,阿基米德说到:“如果单靠实力,我们决不是罗马人对手。现在若能造出一种新式武器来,或许还可守住城池,以待援兵。”国王一听这话,立即转忧为喜,让阿基米德全权指挥这场守卫战。 两天后,整齐的罗马军团方阵向护城河攻来。突然,城里隐约传来吱呀的响声,接着城头上飞出大大小小的石块,山洪般地倾泻下来。罗马人渐渐支持不住了,连滚带爬地四散逃命。
阿基米德到底造出了什么秘密武器让罗马人大败而归呢? 原来他制造出了特大的弩弓—投石机。这是一种巨大的弓,人是根本拉不动的,他利用了杠杆原理。只要将弩上转轴的摇柄用力扳动,那与摇柄相连的牛筋又拉紧许多根牛筋组成的粗弓弦,拉到最紧时,再突然一放,弓弦就带动载石装置,把石头高高地抛出城外。原来这杠杆原理并不是简单使用一根直棍撬东西。
击败从西北攻城的罗马陆军军团之后,又有战报传来,罗马海军从东南海面上发动了攻势。当罗马战船开到叙拉古城下,士兵们拿着云梯正要往墙上搭的时候,突然城头上伸出了几副木头架子,木架上垂下一条条铁链,链头上有铁钩、铁爪,钩住了罗马海军的战船。任水兵们怎样使劲划桨,用刀砍,用火烧,大铁链分毫无损,战船不能挪动半步。正当船上一片惊慌时,只见大木架上的木轮又“嘎嘎”地转动起来,铁链越拉越紧,船渐渐地被吊起离开了水面。随着船身的倾斜,士兵们纷纷掉进了海里,桅杆也被折断了……阿基米德的这些"怪物"原来也是利用了杠杆原理,并加了滑轮。 事件真相
“给我一个支点,我就能撬起地球!”,这是古代发现杠杆原理的阿基米德说的话。阿基米德知道,如果利用杠杆,就能用一个很小的力,把非常重的东西举起来,只要把这个力放在杠杆的长臂上,而让短臂对重物起作用。
然而如果这个古代伟大科学家知道了地球的质量,他也许就不会这样夸口了。让我们设想阿基米德真的找到了另一个地球做支点;再设想他也做成了一根够长的杠杆。你知道他得用多少时间才能把质量等于地球的一个重物举起,哪怕只举起1cm呢?至少要30万亿年!
如果一个人只能直接举起60kg的重物,那么他要“举起地球”,就得把自己的手放在一根这样长的杠杆上,他的长臂应当等于它的短臂的倍。 简单地计算一下就可以知道,在短臂的那一头举高1cm,就得在长臂那一头在宇宙空间里画一个大弧形,弧的长度大约是:m。 这就是说,阿基米德如果要把地球举起1cm,他那扶着杠杆的手就得移动大到这样不可想象的一个距离!那么他要用多少时间才能做完这件事呢?如果我们认为阿基米德能在一秒中里把60kg的重物举高一米(这种工作能力已经几乎等于一马力!),那么,他要把地球举起1cm,就得用去 秒,即三万亿年!可见阿基米德根本无法完成这个任务。 关于撬起地球还有另一种解读,阿基米德说的是撬起地球,而不是说撬起地球1cm。他在长杠杆的另一头,只需要撬动1m,相应的地球也会移动m,地球移动的距离可能很短很短,但是不管如何,地球还是动了。 [1] 王宝琪 . 阿基米德与杠杆 : 《数学大世界(上旬)》杂志 ,2014-8
[2] 杠杆原理在数学里怎么用 · 好二三四[引用日期2022-11-30]
金字塔数百万块巨石,是如何搭建的?从阿基米德的杠杆原理讲起