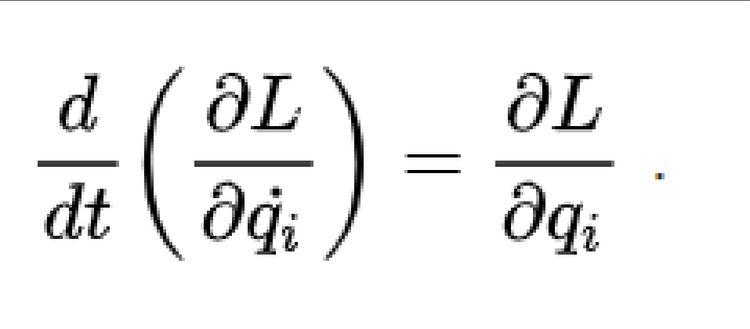精选百科
本文由作者推荐
小编整理：
拉格朗日量是经典力学中的一个重要概念，它是一种函数，用于描述系统的运动状态和演化过程。拉格朗日量在分析力学中有着广泛的应用，可以用来研究物体的运动轨迹、动量、能量、角动量等物理量之间的关系。 拉格朗日量的建立是由拉格朗日在1788年完成的，它是一种对经典力学的新数学表述。通过引入拉格朗日量，可以将系统的运动描述从一个几何空间转移到数学空间，从而更加方便地进行数学分析和计算。 拉格朗日量的建立是基于一些基本的假设和推导，它能够描述系统的运动轨迹和物理量之间的关系，可以用来解决一系列实际问题。例如，在力学、天文学、机械工程等领域中，拉格朗日量都有着广泛的应用。 总之，拉格朗日量是经典力学中的一种重要函数，它为研究物体的运动、物理量之间的关系提供了有力的工具，并在多个领域中得到了广泛的应用。拉格朗日量
1788年拉格朗日建立的函数
拉格朗日量的建立人
来源
1788年，约瑟夫·拉格朗日建立拉格朗日力学，是对经典力学的一种的新的理论表述，着重于数学解析的方法，是分析力学的重要组成部分。它有一个基本假设是具有 n 个自由度的系统，其运动状态完全由 n 个广义坐标及广义速度决定。力学系统的运动状态由一个广义坐标和广义速度的函数描述：此函数即拉格朗日量（函数）。
生平介绍
约瑟夫·拉格朗日
约瑟夫·路易斯·拉格朗日（Joseph-Louis Lagrange 1735~1813）
法国数学家、物理学家。1736年1月25日生于意大利都灵，1813年4月10日卒于巴黎。他在数学、力学和天文学三个学科领域中都有历史性的贡献，其中尤以数学方面的成就最为突出。
拉格朗日生平
拉格朗日1736年1月25日生于意大利西北部的都灵。父亲是法国陆军骑兵里的一名军官，后由于经商破产，家道中落。据拉格朗日本人回忆，如果幼年是家境富裕，他也就不会作数学研究了，因为父亲一心想把他培养成为一名律师。拉格朗日个人却对法律毫无兴趣。
到了青年时代，在数学家雷维里的教导下，拉格朗日喜爱上了几何学。17岁时，他读了英国天文学家哈雷的介绍牛顿微积分成就的短文《论分析方法的优点》后，感觉到“分析才是自己最热爱的学科”，从此他迷上了数学分析，开始专攻当时迅速发展的数学分析。
18岁时，拉格朗日用意大利语写了第一篇论文，是用牛顿二项式定理处理两函数乘积的高阶微商，他又将论文用拉丁语写出寄给了当时在柏林科学院任职的数学家欧拉。不久后，他获知这一成果早在半个世纪前就被莱布尼兹取得了。这个并不幸运的开端并未使拉格朗日灰心，相反，更坚定了他投身数学分析领域的信心。
中年时的约瑟夫·拉格朗日1755年拉格朗日19岁时，在探讨数学难题“等周问题”的过程中，他以欧拉的思路和结果为依据，用纯分析的方法求变分极值。第一篇论文“极大和极小的方法研究”，发展了欧拉所开创的变分法，为变分法奠定了理论基础，变分法的创立，使拉格朗日在都灵声名大震，并使他在19岁时就当上了都灵皇家炮兵学校的教授，成为当时欧洲公认的第一流数学家。1756年，受欧拉的举荐，拉格朗日被任命为普鲁士科学院通讯院士。
1764年，法国科学院悬赏征文，要求用万有引力解释月球天平动问题，他的研究获奖。接着又成功地运用微分方程理论和近似解法研究了科学院提出的一个复杂的六体问题(木星的四个卫星的运动问题)，为此又一次于1766年获奖。
1766年德国的腓特烈大帝向拉格朗日发出邀请时说，在“欧洲最大的王”的宫廷中应有“欧洲最大的数学家”。于是他应邀前往柏林，任普鲁士科学院数学部主任，居住达20年之久，开始了他一生科学研究的鼎盛时期。在此期间，他完成了《分析力学》一书，这是牛顿之后的一部重要的经典力学著作。书中运用变分原理和分析的方法，建立起完整和谐的力学体系，使力学分析化了。他在序言中宣称：力学已经成为分析的一个分支。
这期间他参加了巴黎科学院成立的研究法国度量衡统一问题的委员会，并出任法国米制委员会主任。1799年，法国完成统一度量衡工作，制定了被世界公认的长度、面积、体积、质量的单位，拉格朗日为此做出了巨大的努力。
1791年，拉格朗日被选为英国皇家学会会员，又先后在巴黎高等师范学院和巴黎综合工科学校任数学教授。1795年建立了法国最高学术机构——法兰西研究院后，拉格朗日被选为科学院数理委员会主席。此后，他才重新进行研究工作，编写了一批重要著作：《论任意阶数值方程的解法》、《解析函数论》和《函数计算讲义》，总结了那一时期的特别是他自己的一系列研究工作。
L1
例如：一个围绕太阳旋转的物体，它距太阳的距离越近，它的轨道周期就越短。但是这忽略了地球的万有引力对其产生的拉力的影响。如果这个物体在地球与太阳之间，地球引力的影响会减弱太阳对这物体的拉力，因此增加了这个物体的轨道周期。物体距地球越近，这种影响就越大。在L1点，物体的轨道周期恰好等于地球的轨道周期。太阳及日光层探测仪（SOHO）（NASA关于SOHO工程的网站 ）即围绕日-地系统的L1点运行。
L2
在两个大天体的连线上，且在较小的天体一侧。
例如：相似的影响发生在地球的另一侧。一个物体距太阳的距离越远，它的轨道周期通常就越长。地球引力对其的拉力减小了物体的轨道周期。在L2点，轨道周期变得与地球的相等。
L3
在两个大天体的连线上，且在较大的天体一侧。
例如：第三个拉格朗日点，L3，位于太阳的另一侧，比地球距太阳略微远一些。地球与太阳的合拉力再次使物体的运行轨道周期与地球相等。
L4
L5
在以两天体连线为底的等边三角形的第三个顶点上，且在较小天体围绕较大天体运行轨道的后方。
L4和L5有时称为“三角拉格朗日点”或“特洛伊点”。
定义
拉格朗日量（又称拉格朗日函数）是动能T 与势能V 的差值。通常，动能的参数为广义速度（符号上方的点号表示对于时间t的全导数），而势能的参数为广义坐标，所以，拉格朗日量的参数。
方程
假设一个物理系统的拉格朗日量为，则此物理系统的运动，以拉格朗日方程表示为
粒子物理应用
拉格朗日量方法的优点在于，它是一个微扰理论，这个理论不仅包括了树图能级贡献，而且也包含了圈贡献。目前，这样的计算只能对结果的数量级进行估计，因为没有充足的实验数据去确定拉格朗日量抵消项的任意系数。然而，它们提供了一个圈图贡献大小的线索。我们将介绍与此相关的两个例子：第一个是超精细质量劈裂下圈效应的大小。第二个例子是通过手征的圈效应给出比率，其中fDs和Df 分别为介子和 介子的轻子衰变常数。计算手征圈效应的其它例子还包括对强耦合常数的修正，对半轻子的形状因子的修正和以及对B介子和 D介子辐射衰变与稀有衰变的修正。
有效拉格朗日方法最主要的缺陷是在拉格朗日量中有大量的耦合常数。即使在轻介子微商和1Qm展开的最低阶，不得不使用数据确定几个耦合。一个典型的例子是已经提及到的D*Dπ耦合常数，目前确定它的实验数据仍不充足。在缺少实验数据的情况下，人们也可以依靠理论研究提供的结果，比如来自 求和规则或势模型关于它的或者 晶格模拟。另一个可选择的办法是不仅通过强相互作用，而且通过介子之间的弱相互作用和电磁相互作用获取相关信息。事实上，手征拉格朗日量在这些过程中的应用不仅为决定体系的耦合常数提供了可能，而且提供了由对称联系的不同过程之间的定量关系。要做到这一点，通常使用两种方法：第一种方法是用手征对称性和重夸克味对称性联系不同弱跃迁和电磁跃迁的振幅之间的关系。第二种方法是利用手征拉格朗日量来计算不同的振幅。无论使用哪种方法，都需要对形状因子的q²行为做出一些假设。
拉格朗日量相关的文章
晏晓陶，女，原TVB国语配音演员，曾为多部电视剧和电影进行配音。她的代表作品包括《神雕侠侣》《冤家易结不易解》《梁祝》以及2004年的《金枝欲孽》中的安茜。1994年，她为《梁祝》中的杨采妮配音，1996年为电影《甜蜜蜜》中的张曼玉配音。晏晓陶的丈夫是香港男高音歌唱家、国语配音演员黄河，他最为人所知
矢泽爱（日文：矢沢 あい），日本漫画家、插画家，1967年3月7日出生于日本兵库县。主要作品有《一起去吹吹风》《天堂之吻》《娜娜》《近所物语》《圣学园天使》等。
不列颠群岛是欧洲西北部的岛群。包括大不列颠和爱尔兰两个主要岛屿以及许多小岛在北海与大西洋之间，东南以英吉利海峡、多佛尔海峡与欧洲大陆相望。包括大不列颠和爱尔兰两大岛，以及附近的赫布里底群岛、奥克尼群岛、设得兰岛、安格尔西岛和马思岛等，约5，000个小岛。总面积31.5万平方公里。
阿姆斯特丹（Amsterdam），荷兰首都及最大城市，人口约110万，位于荷兰西部的北荷兰省。享誉世界的旅游城市和国际大都市，在最新的世界城市排名权威机构GaWC中名列欧洲第三，仅次于伦敦和巴黎。
山西本词条是多义词，共3个义项中华人民共和国省级行政区山西，简称“晋”，中华人民共和国省级行政区，省会太原，位于中国华北，东与河北为邻，西与陕西相望，南与河南接壤，北与内蒙古毗连，介于北纬34°34′—40°44′，东经110°14′—114°33′之间，总面积15.67万平方千米。山西省地势呈东北斜向西南的平行四边形，是典型的为黄土覆盖的山地高原，地势东北高西南低。高原内部起伏不平，河谷纵横，地
尚可名片
这家伙太懒了，什么都没写！
作者
