精选百科
本文由作者推荐
小编整理：
光速是物理学中的一个重要常数，它表示光在真空中传播的速度。以字母c表示，其值为299,792,458米/秒。这个速度是电磁波在真空中的速度，也是所有电磁波在真空中传播的速度极限。 光速在许多物理学定理和现象中都起着重要的作用。根据狭义相对论，光速是宇宙中所有物质运动的极限速度，任何物体都无法以超过光速的速度移动。此外，光速还与时间、空间和引力等概念密切相关。 除了在物理学中的重要性，光速还在其他领域中有广泛的应用。例如，在通信领域中，光速是光纤通信和卫星通信的基础。在光学领域中，光速也是非常重要的，因为许多光学现象都与光速有关。 总之，光速是物理学中的一个非常重要的常数，它与许多定理和现象都有着密切的联系，并在许多领域中有广泛的应用。光速
通用物理常数
光速是一个物理常数，指真空中光和其他电磁波的速度。通常以英文字母 c 表示，真空中光速也称为自由空间中光速。无线电波、X射线等电磁波都以光速传播。光波传播的速度，与力学、电磁学、光学及近代物理中的许多定理都有着极为密切的联系。光速是目前科学界所发现的速度极限，根据狭义相对论光速是宇宙中所有的物质运动或能量（以及携带的信息）在空间中传播的速度上限，也是所有无质量粒子及对应的场波动在真空中运行的速度。这由电子在电子加速器中被加速时的一些实验结果得到了证实。在相对论中，光速c与空间和时间相关联，在质能等价方程中具有特殊意义。在特定情况下，物体或波的传播速度可能比光速更快（例如，波的相速度、某些高速天文物体的出现以及特定的量子效应）。
基本信息
中文名
光速
英文名
Lightspeed / speed of light / velocity of light / electromagnetic constant
相关著作
《相对论》
相关性质
1．光速的绝对性：光速是极限速度，以光速运动的粒子的引力质量为0
2．光速是一种标量速度，在各个方向上大小相等
3．光速同任何速度相加之和仍为光速。光速与任何速度（亚光速、光速或超光速）的合成速度仍是光速
4．光速的不变性：对于同一个参照系，光速值为常数，与光源的运动状态和方向无关
不同介质
光的波长
不同介质中光速的计算方法：令
若介质的折射率随光波频率变化很大，群速度就会变得很小。所以，在小频率范围内介质的折射率发生急剧变化是实现光速减慢的关键。
机制原理
一般的牛顿第二定律是：当力F作用于质量为m的物体上时，所产生的动量mv的变化率等于这个力，即F＝
m=
其中c是光速，m0是粒子的静止质量。设M＝m-m0是粒子质量的增量，则其能量的相应增量E为粒子所受力F对它所作的功，即E=
由 (1)有m=
由 (2)有E=
=m0c
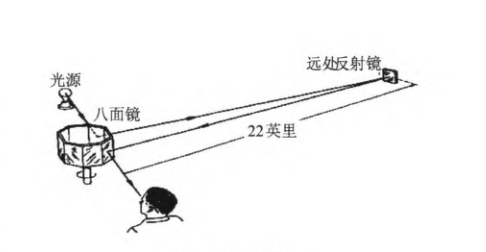
研究历史
亚里士多德坚信光不会移动，只存在出现与否的差异，这一观点得到当时许多人的支持。古希腊人认为，视觉对于光传播的感知是从眼球指向被观测物体的。但是亚历山大的海伦（Heronof Alexandria）认为：若当真如此，那么光的传播必然是瞬时的，否则当我们睁开眼睛时，又如何能瞬间看到远方的星体。伊斯兰学者阿尔哈曾（Alhazen）著有《光学宝鉴》（Book of Optics），他认为光是从相反方向传播而来，是从被观察物体传播到观测者眼中的。
意大利物理学家伽利略认为，只要光的传播需要时间，人类就能测算出光速。1607年，36岁的伽利略进行了世界上第一个测量光速的实验。他提出通过计量光信号传播时间来计算光速的方法：一人带着时钟和提灯站在一座山丘上，另一人也拿着提灯站在邻近且距离已知的另一山丘上。第一人打开灯时开始计时，第二人看到光后，打开自己的灯，第一人看到第二人的灯光时，停止计时。为了使光传播距离较远，测定误差较小，他让两个人分别站在两座山上。由于伽利略测量光速所用的距离过短，不足以精确测量出光线传播时长，所以实验以失败告终。法国数学家笛卡尔对此实验做了进一步改良，他认为：若光线从太阳或月球传播到地球需要时间，那月食等现象真实发生的时刻就会和人类的预测存在差别。但经过多次观测，仍未发现任何时滞。事实上，伽利略和笛卡尔的思路是正确的，但由于光线传播速度极快，穿过月地距离和日地距离的时间十分短暂，当时的实验器材不足以观测出来。
1676年，丹麦天文学家奥勒·罗默（OIaus Roemer）第一次提出了有效的光速测量方法并成功运用“木星卫星法”计算出了光速。他在巴黎对木星的一个卫星木卫一的掩星研究观测发现：它的掩星发生时间与预期时间不符。地球靠近木星时，掩星早11分钟；地球距木星较远时，掩星晚11分钟。并且在地球处于太阳和木星之间时的周期与太阳处于地球和木星之间时的周期相差十四、五天。他认为这种现象是由于光具有速度造成的，他还推断出光跨越地球轨道所需时间为22分钟。1676年9月，罗默预言预计11月9日上午5点25分45秒发生的木卫食将推迟10分钟。观测最终证实了罗默的预言。结合木星距离，罗默估算出光速约为2.1
1725年，英国天文学家詹姆斯・布拉德雷（James Bradley）发现了恒星的“光行差”现象，以意外的方式证实了罗默的理论。一开始，他无法解释他观测到的这一现象，直到1728年，他在坐船时受到风向与船航向相对关系的启发，认识到光的传播速度与地球公转速度共同引起了“光行差”的现象。他用地球公转的速度与光速的比例估算出了太阳光到达地球需要8分13秒。布拉德雷测定值证明了罗默的光速有限性的说法。
1849年9月，法国人斐索（A.H.Fizeau）用旋转齿轮法测得光速为3.153
1928年，美国物理学家阿尔伯特・迈克尔逊为了测定出误差在0.001%以内，精确程度满足最基本的核物理运算的光速值，已经在过去50多年内设计了12次实验。他发明了6台精密装置，最终准确地测定出光速。并因此获得了诺贝尔奖。迈克尔逊用一个能够恒速旋转的引擎驱动八边形棱镜高速旋转，他向棱镜照射光线，在镜子旋转到某点时，光束正好能够反射到屋子后墙上静止的曲面镜上。这面旋转的镜子只用远远少于1秒的时间就能够把光线反射回曲面镜上，然后又继续旋转。曲面镜从棱镜的每面都会收到短光脉冲。每个光脉冲经过聚焦透镜的反射，穿过墙洞，传播到22英里外的圣·安东尼山上。在那里，经过第二个聚焦透镜的反射，光脉冲又从一面镜子上径直返回鲍尔迪山。在这里，光脉冲又照射到后墙的曲面镜上，最后反射到旋转镜上。每个光脉冲不到1/4000秒就完成44英里的路程。返回光线在棱镜的反射下，就会投射到栅屋墙上的一个点。通过从棱镜与这一点的角度，迈克尔逊可以计算出光脉冲完成44英里往返路程，镜子转动的角度，并以此计算出光速。迈克尔逊计算出光速是2.997950377
20 世纪初，两位科学家从理论上推算出光速的数值。1906 年，罗萨（E.B.Rosa）和窦赛（N.E.Dorsey）发表了一个准确的光速值：299784±15 km/s。这个数值是他们通过测量两类电单位之比，即绝对静电单位(esu)中的电荷与绝对电磁单位(emu)的同一电荷之比获得的。1941年，伯奇(R.T.Birge)评论此实验为“整个科学史上精密研究中完成的最美的实验之一” 。二人测量的光速值处于当时光速测量值的中间值，与2.99774
1924年，卡罗卢斯（Karolus）和米特尔施泰特（Mittelstaedt）提出利用克尔盒法来测定光速。1934年，谷瑞·德布雷（Cheury de Brayza）发表了有关光速的文章，其中列出了他们几年间光速的测量结果：1924年的结果为2.99802
20世纪50年代流行用微波法测定光速，1958年有一个较精确的光速值是在微波干涉仪（f=72GHz）中获得的：c=2.99792500
1973年6月，国际计量局（BIPM）米定义咨询委员会决定以高精度光频测量和高精度光波长为基础：取激光波长
但光速还定义着比长度更加基本的东西。阿尔伯特·爱因斯坦（Albert Einstein）的工作表明了光速的真正重要性。他证明光速不仅仅是光子在真空中运动的速度，还是连接时间与空间的基本常数，不过，一直与相对论有冲突的量子理论是允许物质以大于光速的速度运动的。在20世纪20年代，量子论显示一个系统相隔遥远的不同组成部分能够瞬时联系。1993年，加利福尼亚大学伯克利分校的Raymond Chiao表明，量子理论还允许另一种超光速旅行存在：量子隧穿。德国物理学家维纳·海森堡的测不准原理表明：在一个系统中，总有某些属性，在这一情况中是能量的值是不能确定的，只能确定在一个区间内，因此量子物理学原理允许系统利用这种不确定性，短时间借到一些额外的能量。在隧穿的情况中，粒子从障碍物的一面消失又从另一面重现的需要几乎可以忽略不计。不过随着厚度增加，粒子隧穿的几率也就迅速地朝零的方向递减，但不会等于0（如若这样，海森堡原理就会被反对）。Chiao通过测量可见光光子通过特定过滤器的隧穿时间，证明了隧穿“超光速”的隧穿效应存在。为此，他让这些光子与在相似时间内穿过真空的光子进行比较。结果隧穿光子先到达探测器，Chiao证明它们穿越过滤器的速度可能为光速的1.7倍。2008年8月，《Nature》杂志上，瑞士的塞拉特等5位科学家公布了他们的一项最新研究成果：量子信息传输速度远超光速。瑞士科学家对相互纠缠的光子进行了实验研究。通过对其中一个光子的分析，科学家可以预测另一光子的特征。在实验中，任何隐藏信号从此接收站传送到彼接收站，仅仅需要一百万兆分之一秒。由此可以推测任何未知信号的传输速率至少是光速的1万倍。
测定方法
经典物理测定方法
旋转棱镜法
旋转棱镜法
棱镜不转动时，只有八棱镜的某一面恰好与人射光线成45度角时，光线能被反射至远方的反射装置，反射回来的光线经另一面反射进入观察者眼睛，观察者能看到光源的像。棱镜以较小的转速转动时，光线经1号面和反射装置反射后到达棱镜时，3号面已经不再与光线成45度角，光线无法进入观察者眼睛，观察不到光源的像。若缓慢提高棱镜转速，当光线反射回棱镜时，棱镜刚好转过1/8转，即2号面转至原3号面所在位置，则光线又可以进入观察者眼睛，重新看到光源的像。
棱镜转速只有在目标转速附近极小的范围内可以看到光源的像，其他转速下均观察不到光源的像。在此实验中，实验现象稍纵即逝，很难被观察到。一旦被观察到，对应的转速会比较精确，测量结果精度较高。
旋转齿轮法
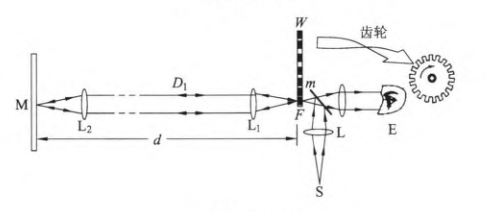
旋转齿轮法
实验中选用齿宽和齿间缝宽相等的齿轮，当齿轮匀速转动时，光线周期性被齿轮遮挡，这些光线由反射装置反射回齿轮处时，具有一定的延时，返回的光线被齿轮部分遮挡，若进一步提高齿轮转速，则齿轮透光时间和挡光时间均减小，反射光线中被遮挡的比例增大。当其减小到刚好等于光线反射延时，反射光线刚好全部被遮挡，观察者刚好看不到光源的像。
齿轮转速在接近目标转速的过程中，看到光源的像逐渐变暗，转速超过目标转速后，像又逐渐变亮。在此实验中，实验现象容易被观察到。但在目标转速附近，像的亮度小到观察者无法识别时会和目标状态混为一体，于是目标转速的不确定度便增大了，降低了实验精度。
近代物理测定方法
微波谐振腔法
1950 年，埃森（Essen）提出用空腔共振法来测量光速。原理是：微波通过空腔时，根据空腔的长度可以求出谐振腔的波长，把谐振腔的波长换算成光在真空中的波长，由波长和频率的乘积可计算出真空中光速。在实验中，将微波输入到圆柱形的谐振腔中，当微波波长和谐振腔的几何尺寸匹配时，谐振腔的圆周长
微波干涉仪法
1952年至1954年，英国国家物理研究所（NPL）的弗洛姆（Froome）用微波干涉仪测定了真空中光速值。通过微波干涉仪测定波长和频率计算出光速。
光电测距仪法
用光在被测基线(约10km)内的飞行时间测定，是伽利略试验的发展。1949年至1957年，瑞典的贝奇斯传德采用了光电测距仪的方法，他用经过调制的克尔盒作为光源，用同一振荡器调制的光电倍增管作为检测器测定光速。
现代物理测定方法
光拍频法
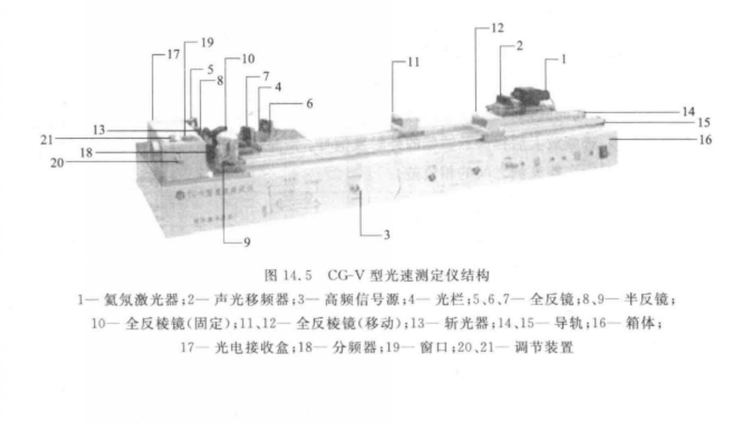
CG-V型光速测定仪
用光电检测器接收这个拍频波，即得频率为拍频，如果接收电路将直流成分滤掉，即得纯粹的拍频信号在空间的分布。这就是说，处在不同空间位置的光检测器，在同一时刻有不同位相的光电流输出，利用比较相位的方法间接测定光速。
光拍频法测量光速是利用声光频移法形成光拍 ，通过远 、近光路产生光程差，测量光拍频率和光拍波长，从而间接测定光速的方法。实验需要测量的数据为拍频波长。测量时需要注意要对光路非常熟悉，并且充分理解光的反射路线，否则测量误差较大。当测出拍频波长后，从数字频率计读出高频信号发生器的输出频率，计算光速。
高精度时间间隔测量
光速的测定可利用v=l/
相关理论
光速不变原理
1905年，爱因斯坦在创立狭义相对论的第一篇论文《论运动物体的电动力学》中提出了光速不变公设：“光在空虚空间里总是以确定的速度v传播着，这速度同发射体的运动无关”。爱因斯坦依据迈克尔逊-莫雷实验，提出光速不变性（ invariance of light speed，ILS）假设，从而在理论上导出洛伦兹变换，建立狭义相对论（special relativity，SR），揭示了时空和物质运动的相对论性。没有物体的运动速度能够超过光速。光速是极限，不存在比光速更快的速度。狭义相对论( SR) 赋予光速非常特殊的性质，一是 “光速不变”原理，二是“光速不可超过”原则。
1887 年，因麦克斯韦的建议，迈克尔逊和莫雷开展了一项捕捉以太的实验。当时的物理理论认为，光的传播介质是“以太”，由此产生一个问题：地球以每秒30公里的速度绕太阳运动，就必然迎面受到每秒30公里的“以太风”，从而必然对光的传播产生影响。这个问题出现以后，立即引起人们探讨“以太风”存在与否。迈克耳孙－莫雷实验就是在这个基础上进行的。他们在实验中没能发现以太，却发现了一个问题：伽利略速度叠加原理失效了。迈克尔逊-莫雷实验显示，光速与地球轨道速度叠加，仍然是光速。为了解释迈克尔逊-莫雷实验，菲兹杰拉德提出一个假设：运动物体沿运动方向长度收缩，收缩率为
光速不变原理又称真空光速极限原理，包含三项内容：光速与光源运动与否无关；光速与频率大小无关；光速与方向（即接受者的速度）无关。现有光学实验确切验证了以上内容的前两项，第三项光速与方向无关这点始终未被证实。利用此原理创立了狭义、广义相对论及超弦理论。光速极限原理是狭义相对论的预言，已被多个实验证实，是物理学基本原理之一。
光速可变理论
2015年1月，英国 Glasgow 大学的研究团队经两年半努力做成功一项实验，证明光速并非恒定不变，亦即光并不总是以光速传播，即使在真空条件下也是如此。 研究论文从在预印本网站 arXiv出现到在美国《Science Express》上刊登只经过几天时间，而且迅即被各国媒体传播报导。1月22日，D. Giovannini 等的论文发表在《 Science Express》上。同日，英国广播公司(BBC)公布了对学术带头人 M. Padgett 教授的采访。 1 月 27 日，中国新闻网发表一个简短报道，标题是“英国科学家成功降低真空中光速,或将颠覆 Einstein 理论。”
在天文学中，光行差现象早已证明了光速与方向有关。对3K微波辐射及对射电星系的无线电波进行的观测均发现了在地球运动方向有明显的各向异性。2002 年3月14日出版的《Nature》杂志报道了牛津大学的C.BIake和J.Wa用美国国家天文台位于新墨西哥州的甚大阵列射电望远镜（VLA）观测了发出强大电波的遥远射电星系，观测结果：他们发现这些星系发出的电磁波同样在地球运动方向上表现出了各向异性，这种各向异性与上述宇宙背景辐射在地球运动方向上的各向异性是相同的。电磁波（即光波）速度随观测者（地球）速度的不同而发生变化。这些天文学实验确切地证明了光速与方向是有关的，因此光速可变是一个合理的结论。光速可变理论认为光速与接受者密切相关，即观测者的速度将直接影响接受者所测得的光速：与光同向运行的接受者测得的光速要变小。与光逆向运行的接受者测得的光速将要变大。而相对于绝对坐标系而言光速是不变的。
光速相关的文章
哈马丹（波斯语： همدان），中亚古城，古称埃克巴坦纳（Ecbatana），伊朗哈马丹省省会，丝绸之路上的一个重要站点。人口550,284人（2005年）。根据亚述的历史记载，哈马丹建成于约公元前1100年，但是一些历史学家认为这个时间还可以上推到前3000年左右。哈马丹曾是米底的首都，也是阿赫美
拉斯维加斯（LasVegas）是美国内华达州最大的城市，也是座享有极高国际声誉的城市。拉斯维加斯建市于1905年5月15日，因位于内华达州的沙漠边缘、边境，所以拉斯维加斯全年高温。
动脉粥样硬化动脉硬化的血管病动脉粥样硬化是一组称为动脉硬化的血管病中最常见、最重要的一种。本病多见于40岁以上的中老年人，男性多于女性。人体中正常的血管是富有弹性的，当血管发生老化、衰退时，血管内脂肪及类脂等物质聚集成斑块，呈黄色粥样，斑块越来越多，会使血管壁增厚变硬，失去弹性，管腔缩小，形成动脉粥样硬化。动脉粥样硬化发生在冠状动脉，则可引起心绞痛、心律失常、心肌梗死；还可发生在脑、肾、下肢动脉，
尚可名片
这家伙太懒了，什么都没写！
作者
