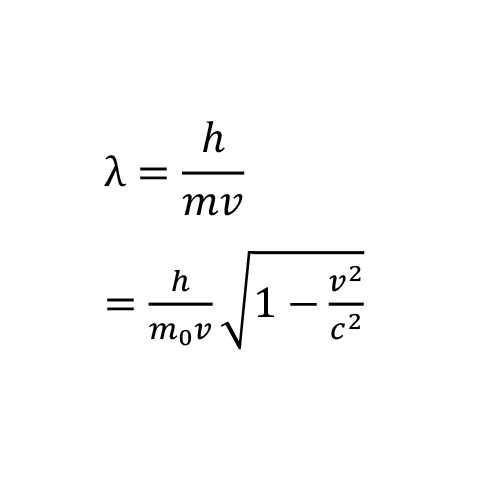物质波公式,又叫德布罗意公式,具体表达式为:波长入=h/p=h/mv,是法国著名物理学家德布罗意推出的物质波动方程。1923年,法国著名物理学家德布罗意经过计算,得出了电子是一种波动的结论,并把这种波称为相波。后人为了纪念他,又称其为“德布罗意波”。此后,基于相波,德布罗意经推导后得到了物质波公式。
精选百科
本文由作者推荐
物质波公式相关的文章
普法战争(英语:Franco-Prussian War),在法国称1870年法德战争(法语:Guerre franco-allemande de 1870),在德国称德法战争(德语:Deutsch-Französischer Krieg),是普鲁士王国为了统一德国,并与法兰西第二帝国争夺欧洲大陆霸权
吉尔吉特-巴尔蒂斯坦(乌尔都语:شمالی علاقے,藏语:གིལྒིཏ་བལྟིསྟན),过去称北部地区(شمالی علاقہ جات),当地民族主义分子称为بلاوارستان,位于巴基斯坦控制的克什米尔的北部,是巴基斯坦最北的地区。面积72,496平方公里,2006年人口1,126,
喀拉塔勒(原译为“哈拉塔”)镇位于阿克苏市的中南部,东与阿拉尔布托喀依乡和温宿县古勒阿瓦提乡接壤,西以阿克苏新大河为界与阿瓦提县相望,南邻向拉尔市抚喀依乡,北接拜什吐格曼乡,地理位置东经80°22′一80°53′,北纬40°31′一40°55′,东西最长31.2千米,南北最宽41千米,距阿克苏市区约49公里,是一个农、林、牧结合的建制镇,全镇总面积11028平方公里,辖区总人口4.51万人,7623户,由维、汉、回等民族组成,镇辖28个行政村、101个村民小组、3个直属农场、22个站〈所),耕地总面积32

尚可名片
这家伙太懒了,什么都没写!
作者