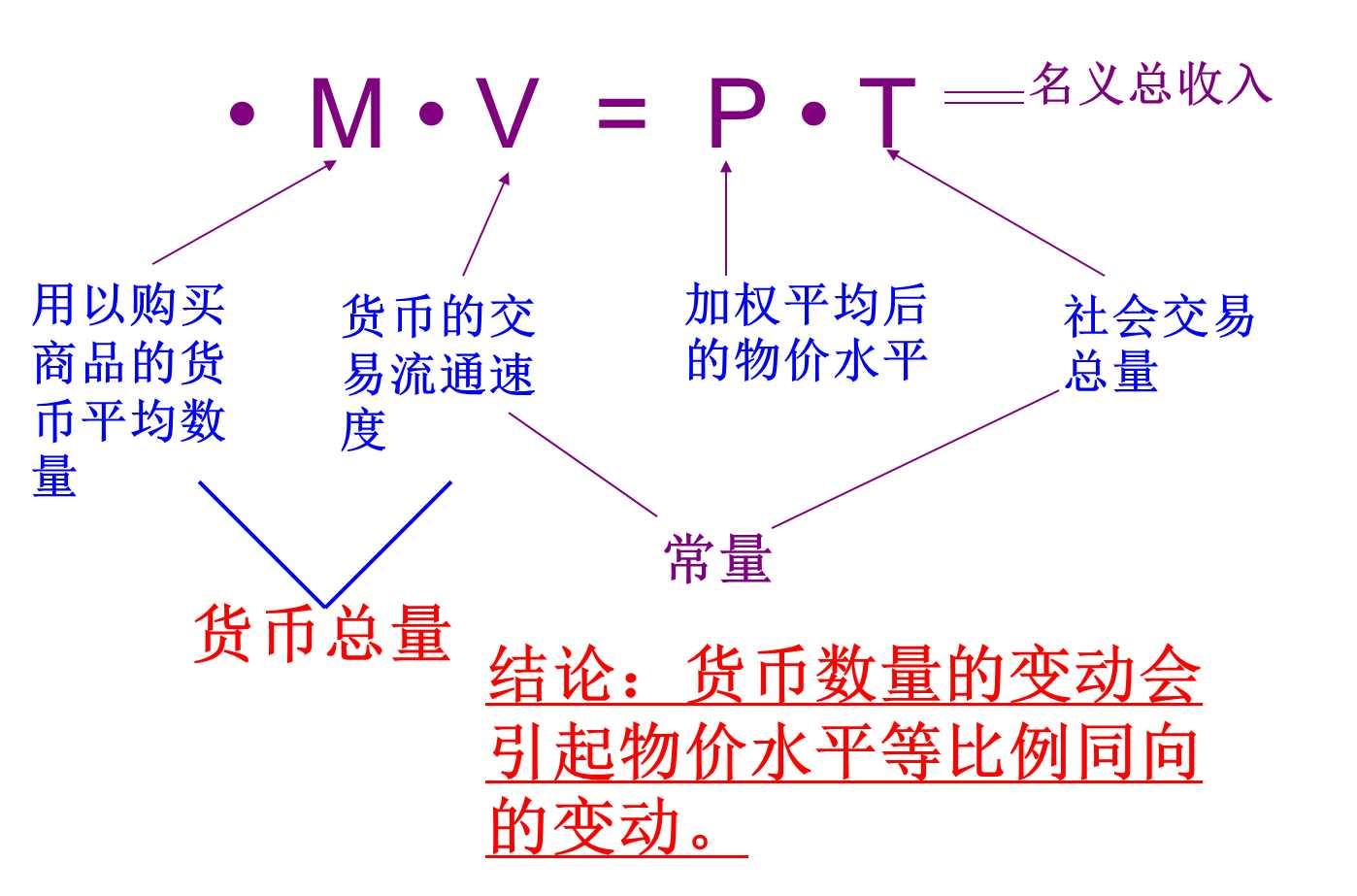
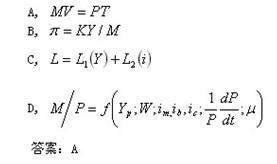方程含义
方程解释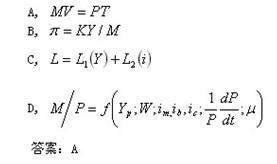
费雪方程式
该方程式表示货币数量乘以货币使用次数必定等于名 义收入。费雪认为,M是一个由模型之外的因素决定的外生变量;V由于由社会制度和习惯等因素决定的,所以长期内比较稳定,视为常数;在充分就业条件下,T相对产出水平保持固定的比例,也是大体稳定的,也可以视为常数。因此只有P和M的关系最重要。这样,交易方程式就转化为货币数量论。而且,货币数量论提供了价格水平变动的一种解释:价格水平变动仅源于货币数量的变动,当M变动时,P作同比例的变动。费雪认为人们持有货币的目的在于交易,这样,货币数量论揭示了对于既定的名义总收入下人们所持的货币数量,它反映的是货币需求数量论,又称现金交易数量论。费雪的货币量方程式MV=PT被认为是经济学的E=MC²,一个揭示了上帝的秘密的工具,一颗学术原子弹。弗里德曼从这个方程式出发构建了蔚为壮观的货币主义大厦,费雪方程式也是现代货币银行学的基础。
一个结论这个方程式的一个结论是:货币量的增加必然引起商品价格的上涨,或者说商品价格的普遍上涨只能是货币引起的。弗里德曼用这个结论把通货膨胀的矛头直接指向货币的发行者——政府,这具有相当的革命意义,从货币主义开始,那些“粮价上涨引起通胀”“战争引起通胀”“工人要求加工资引起通胀”的形形色色的论调就从理论上破产了。通胀的唯一原因就是政府印刷钞票。
货币主义把通胀的原因指向政府的印钞机,这个概念的普及也在很大程度遏制了美国和欧洲发达国家政府印钞的冲动,使得他们的印钞不再那么明目张胆。然而,理论是把双刃剑,货币主义在遏制政府发钞的同时,却在另一个方面支持了政府的发钞,当社会交易量下降、商品价格下跌或者就业率下降的时候,货币主义理论就给了政府以支持:既然政府是通胀的唯一原因,那么当“通缩”这个魔鬼出现的时候,政府就有了印钞票遏制“通缩”的能力和义务。于是“温和通胀”“保持物价稳定”就成了货币主义的政策目标,此时,反对政府干预经济的“货币主义学派”就摇身一变,成了和凯恩斯主义者毫无二致的大政府主义者。
方程意义
本方程揭示了价格的本质,对研究价格定价机理有着奠基石的作用。
MV=PT这个公式当中,M是指货币总量,V是指货币流通速度,P是指商品的平均价格,T是指总交易商品量。
费雪方程一开始提出的应用范围是运用在经济总量的大宏观层面,故上述四个变量都是总量性变量。
方程右侧我们先看P,商品的平均价格,这是什么意思?一筐苹果和一次性交易和一套房子和一堂数学课的平均价格。这里平均价格的概念初看似乎很难让人理解,一筐苹果和一套房子的平均价格似乎没有多大关联。但是考虑到交易方程的宏观意义,你就会知道设定这个变量的价值。比如说在股票市场里有成千上万只股票,有一些可能几百块,有一些可能几块钱。每天股市开盘的时候,也许是几百块的股票在跌,几块钱股票在涨,也可能相反,那么股票市场到底在涨还是跌呢?这时候机会选择看股票价格指数。交易方程里的这个平均价格水平P 就可以看作类似于股票市场里面的指数,其目的是反映出整个社会里所有交易物品的总量价格水平。这在研究总量经济,尤其是通货膨胀或者通货紧缩的时候是非常重要的一个概念。比如说,有人看到猪肉和青菜大涨,就说我们的经济体在经历通货膨胀,但是也许除了这两样东西,衣服,房子,鞋子,一堂数学课的价格都在下跌。那么怎么判定整体物价水平?我们就需要用到交易方程里这个平均价格的概念,只有当这个平均价格在持续不断的上涨,我们才能科学的说,我们的经济体正在经历通货膨胀现象。如果发现平均价格水平没有或反向变动,那么就可以得出结论,上述猪肉和青菜的价格出现了结构性,而非经济总量性变动,从而为政策制定给出指引。比如说,如果将上述猪肉青菜价格上升误认为是通货膨胀,从而对经济整体进行紧缩的货币政策,那么就会导致严重的政策错误从而极大的危害经济发展。
方程左侧M 即货币总量,现在经济体中形形色色的交换介质很多,比如现钞、活期存款、定期存款、信用卡、国库券、粮票、布票、商场代金券、银行汇票、债券,让人看的眼花缭乱。费雪方程从考察总量的角度出发,甄别出货币总量是非常轻而易举的事情。在现代社会中,货币的静态总量就是现金+央行存款准备金+商业银行活期存款这三者的总和,也就是M1。关于这一点的鉴别属于货币定义的简单概念,再此不加赘述,有兴趣的朋友可以查阅货币 定义。因此,这个总量信息是可以通过央行与商业银行报表轻松查阅统计,非常方便。
至于V即流通速度,其实更易于理解的说法是货币周转率。打一个比方我有100元钱,一只西瓜,你有50块钱,一杯可乐。在初始状态下,由我们构成的社会里,货币总量M=100+50=150元。如果我们两个就这样拿着钱什么也不做,没有成交,那么所有物品的价格就都是0。现在我们假设今天我想喝一口可乐,我花了100块钱从你的可乐瓶里喝一口,那么今天整个经济体里M=150因为一共有150块钱,P=100,因为成交一口可乐的价格是100,T=1,因为成交一口可乐,V=2/3(因为150元里,今天有100元进行了交易)。由上述例子可以直观的看出,V的意义在于一定时期内(比如一天)参与交易的货币占货币总量的比例。在现实生活中,每天有无数的人进行着交易进行着货币交换,看似复杂,其实和上面的例子是一样的。M和V的乘积代表了货币供应量这个概念,是静态的货币总量加上时间这个概念后的增量概念。因此说到货币供应量,潜台词里一定是设定了一定时间的期限。V这个概念对于研究宏观经济定价是至关重要的。比如说,如果你家里立刻多出了100万亿人民币,你是不是马上得出结论,社会马上要通货膨胀了?因为M增加了。但是如果我们加一个条件,这100万亿只能看,不能用,那么你的结论呢?你肯定会说这不是白搭。这个问题看似无聊,其实对于研究社会价格总量变化非常的重要,正是因为V的存在,我们是没有办法简单的通过M的改变就轻率的对物价变化下定论。
公式的运用事实上交易方程在微观领域的价值比宏观领域更璀璨。比如,你有100元想在菜场买一个苹果。经过讨价还价,你付了10元。所以M=100,V=0.1,T=1,P=10。你只需要简单的将公式变形一下就可以得到P=MV/T。这就揭示出了价格的根本性真理,即:价格是成交额(货币)与商品的一种比值,它体现了付出货币方与付出商品方的力量对比关系。
之后的许多学派也对交易方程提出了很多各自的新的理解,但基本差别只是对阐述上述四个变量论点不同而已。比如费雪认为V由社会观念和技术决定,是一个变化缓慢的变量,在分析中可以假定为一个固定值。另外的学派会认为V也是会短期大幅波动的,因此不可以假定为一个恒量。但是无论如何的诠释,都无法改变这个公式黄金般的真理。
本质区别
剑桥方程式与交易方程式两者在形式上基本相同,但二者在研究方法上、内容上却有本质的区别;
(1)对货币需求分析的侧重点不同。交易方程式强调货币的交易手段职能,侧重于商品交易量对货币的需求;剑桥方程式强调货币作为一种资产的职能,侧重于收入y的需求。
(2)交易方程式侧重于货币流量分析,剑桥方程式侧重于货币存量分析;
(3)两个方程式对货币需求的分析角度和所强调的决定货币需求因素有所不同。交易方程式是对货币需求的宏观分析,剑桥方程式是从微观角度对货币需求进行分析。
马歇尔和庇古不仅仅将交易水平和影响人们交易方式的制度作为研究人们持有货币的关键要素,还探讨了货币作为财富的一种被人们选择所持有的原因和对货币需求量的影响。既然货币被人们选择所持有,就不能排除利率的影响。但总体来说,剑桥方程式和交易方程式差异很小,体现了货币中性论,即经济中的实物经济和货币经济的“二分法”思想。