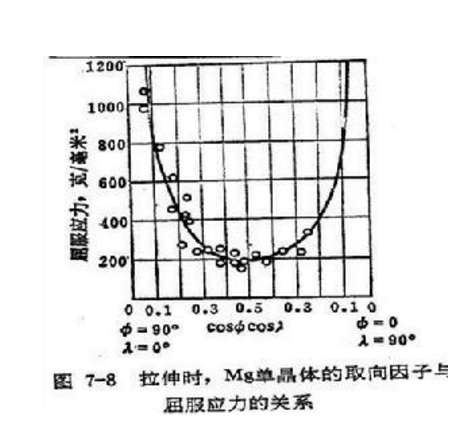
压杆处于临界平衡状态时(F=Fcr ),其横截面上的正应力称为临界应力。不同的压杆一般具有不同的临界应力,临界应力的大小与压杆的长度、截面的形状和尺寸、两端的支承情况以及材料的性质等多个因素有关有关。
精选百科
本文由作者推荐
临界应力相关的文章
国际关系学主要是指研究国际关系行为体之间相互作用,各种国际体系运行和演变规律的一门科学或学问。是政治学的一个分支学科,主要研究领域为战争与和平、合作、一体化、国际组织等国际体系层面的政治现象。国际关系既是学术的领域,也是公共政策的领域。作为政治学的一部分,国际关系也和哲学、经济学、历史学、法学、地理
科尔多瓦(Córdoba)是一个拥有无数文化遗产和古迹的城市。一方面由于它在瓜达尔基维尔河(River Guadalquivir)上的重要战略位置,另一方面由于曾居住在这个城市中的不同民族留下的众多遗迹,科尔多瓦成为了在西方历史的核心地带一个占据特殊位置的城市。其浩瀚的阿拉伯Caliphate(阿拉伯文,直译为继承者国)在中世纪的欧洲是最辉煌的,而这在东方和西方之间架起了永久的桥梁。

尚可名片
这家伙太懒了,什么都没写!
作者