数量曲率(scalar curvature)是里奇曲率的平均。在黎曼几何中,数量曲率(或Ricci标量)是黎曼流形的最简单的曲率不变量。对于黎曼流形上的每个点,它分配由该点附近的歧管的固有几何确定的单个实数。具体来说,标量曲率表示在欧氏空间中,黎曼流形中的小测球的体积与标准球的体积的偏差量。在二维上,数量曲率是高斯曲率的两倍,并且完全表征了曲面的曲率。然而,在两个维度上,黎曼流形的曲率涉及多个功能独立的数量。
数量曲率相关的文章
世界气象组织(英语全称:World Meteorological Organization,简称:WMO),是联合国的一个专门机构,总部设于瑞士日内瓦,有193个会员国和会员地区(截至2023年6月) ,致力于在地球大气状态和变化规律及其与陆地和海洋的相互作用、大气产生的天气和气候、以及由此产生的水
拉斯维加斯(LasVegas)是美国内华达州最大的城市,也是座享有极高国际声誉的城市。拉斯维加斯建市于1905年5月15日,因位于内华达州的沙漠边缘、边境,所以拉斯维加斯全年高温。
拜城县(英文:Bay County),位于新疆维吾尔自治区西南部,阿克苏地区东北部。北依天山与昭苏、特克斯县相连,南隔却勒塔格山与新和县为界,东与库车县毗邻,西与温宿县接壤。总面积15916.81平方千米,根据第七次人口普查数据显示拜城县常住人口为231113人。有维吾尔、汉、回、哈萨克、柯尔克孜等
伊犁哈萨克自治州,中华人民共和国新疆维吾尔自治区下辖州,是中国唯一既辖地区、又辖县市的自治州。总面积26万平方公里,边境线长2000多公里,与哈萨克斯坦、俄罗斯、蒙古等国接壤。“花城”伊宁市是伊犁州的首府。2021年,伊犁哈萨克自治州常住人口为284.84万人。截至2023年4月,伊犁哈萨克自治州下
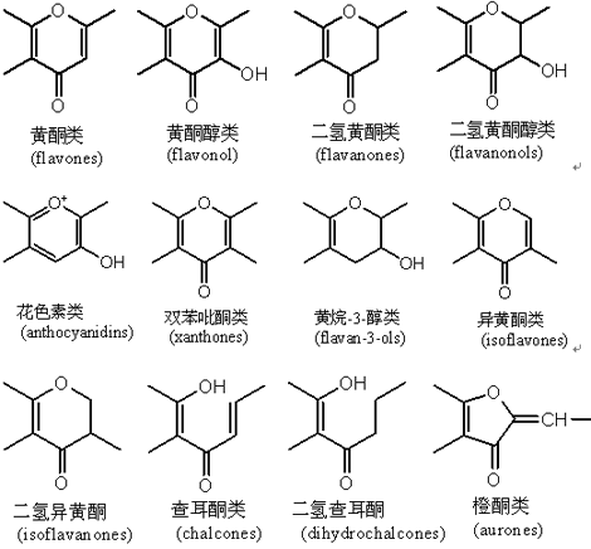
黄酮黄酮类化合物的总称黄酮(flavone),是黄酮类化合物的总称,泛指两个具有酚羟基的苯环(A-与B-环)通过中央三碳原子相互连结而成的一系列化合物。黄酮类化合物结构中常连接有酚羟基、甲氧基、甲基、异戊烯基等官能团。黄酮类化合物(英语:Flavonoid,又称类黄酮)是指基本母核为2-苯基色原酮类化合物,现在则泛指两个具有酚羟基的苯环通过中央三碳原子相互连接的一系列化合物。他们来自于水果、蔬菜、

尚可名片
这家伙太懒了,什么都没写!