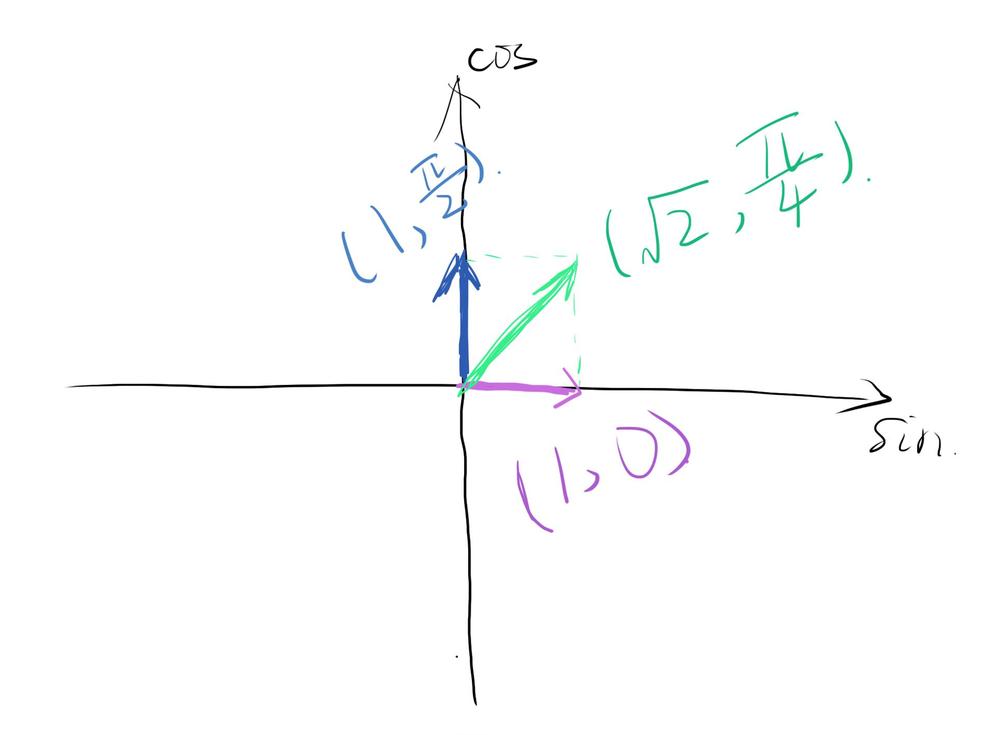
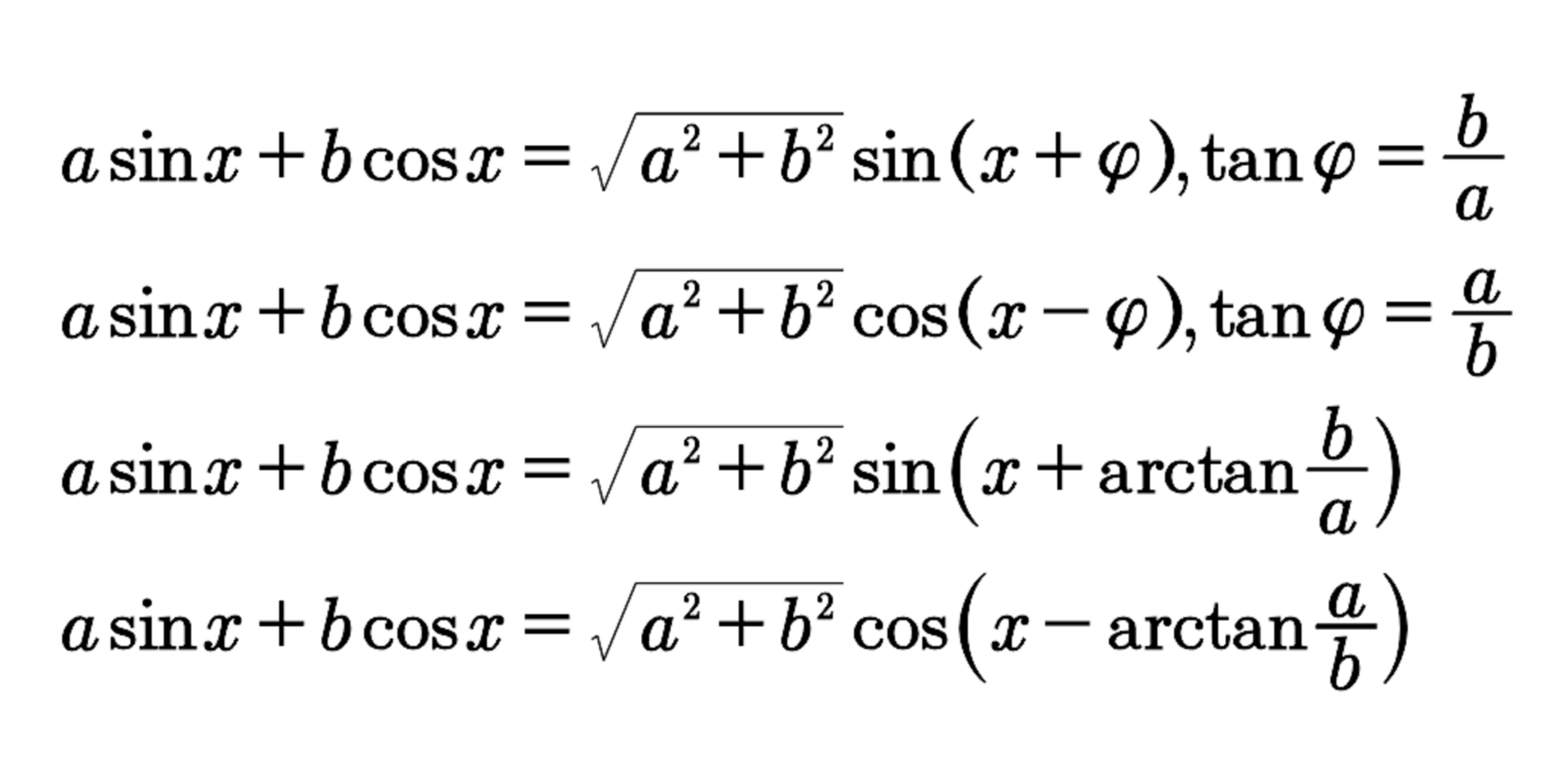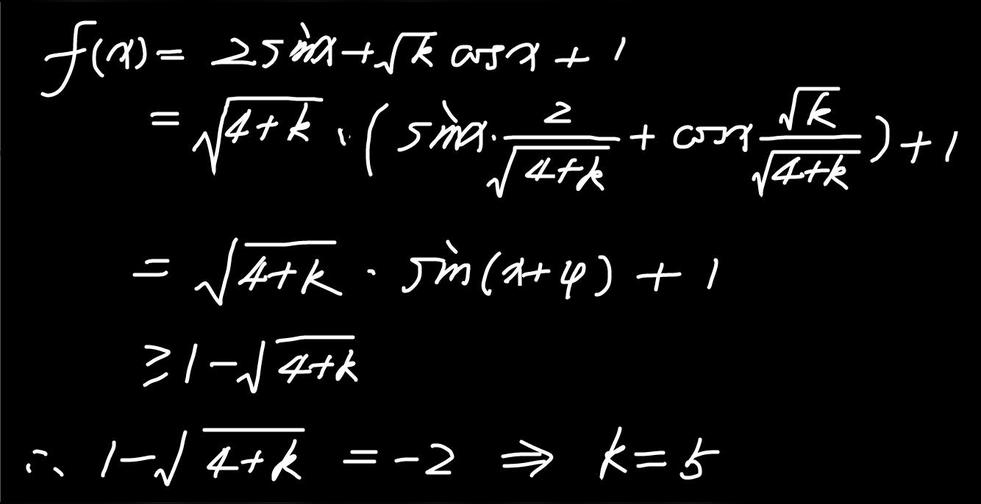辅助角公式是李善兰先生提出的一种三角函数公式,使用代数式表达为asinx+bcosx=√(a²+b²)sin[x+arctan(b/a)](a>0)。虽然该公式已经被写入中学课本,但其几何意义却鲜为人知。
精选百科
本文由作者推荐
辅助角公式相关的文章
巴勒斯坦地区(阿拉伯语: المناطق الفلسطينية ;希腊语:Παλαιστινιακά εδάφη ;希伯来语:השטחים הפלסטיניים;拉丁语:Palestine)是西亚的一个地理区域,位于地中海与死海、约旦河之间,地处亚、非、欧三洲交通枢纽,具有重要的战略意义。面积270
斯瓦尔巴群岛(英语:The Svalbard archipelago)位于北极圈内,北冰洋上,在巴伦支海和格陵兰海之间,南距挪威北海岸657千米,距离北极点1750千米,总面积达62248平方千米,由斯匹次卑尔根、东北地岛、巴伦支和埃季四个岛屿及数十个小岛组成。斯匹次卑尔根是斯瓦尔巴面积最大的岛屿,
辣根(拉丁学名:Armoracia rusticana),又名马萝卜、西洋山葵、山葵大根等,是十字花科(Brassicaceae)辣根属(Armoracia)的多年生草本植物,起源于地中海和东欧,现在中欧、东欧和亚洲等地广泛栽培,中国黑龙江、吉林、辽宁及北京等地有栽培。辣根喜冷凉,耐寒;适宜于土壤深
葡萄酒(汉语世界有时以红酒称之)是经过发酵的葡萄或葡萄汁制作而成的酒精饮料。葡萄酒主要由水和酒精(乙醇)组成,但也有芳香化合物、酸、酚类物质、二氧化碳等其他物质。一般葡萄酒中酒精含量7%到16%(体积分数),但在部分特种葡萄酒中,酒精含量可达20%(体积分数)。

尚可名片
这家伙太懒了,什么都没写!
作者