指数映射(exponential mapping)是由李群的李代数到李群的一种解析映射。若G为李群,e为单位元素,Te(G)为G中点e的切空间，任取Xe∈Te(G),则唯一存在左不变向量场X,使得Xg=dLg(Xe),∀g∈G.

外文名

exponential mapping

所属学科

微分几何

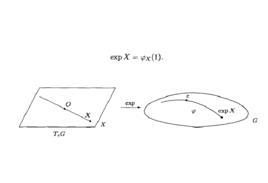
定义

定义一

由李群的李代数到李群的一种解析映射。若G为李群,e为单位元素,T(G)为G中点e的切空间，任取

,则惟一存在左不变向量场X,使得

.任给左不变向量场X,构作算子

任意取定单位坐标邻域U,点

,记

当

为U中点。于是，在U中有一条单参数解析曲线

记

.它可开拓到

,使得

且

为G之一维连通李子群。反之，任意一维连通李子群惟一决定左不变向量场X,使得此李子群为exp(tX).于是，有映射

,称为指数映射，这里J为李群G的李代数。指数映射是建立李群和它的李代数间的关系的重要工具，在李群理论中占有重要的地位.

且

为G之一维连通李子群。反之，任意一维连通李子群惟一决定左不变向量场X，使得此李子群为exp (tX ).于是，有映射

，称为指数映射，这里J为李群G的李代数。指数映射是建立李群和它的李代数间的关系的重要工具，在李群理论中占有重要的地位   .

定义二

切平面到曲面的一种映射。设T是曲面S在P点的切平面，指数映射是从切平面T到曲面S上的一个对应关系，记成

,定义如下：设v是曲面S在P点的一个切向量，过P作S上切于v的测地线，在此测地线上取一点M使得从P到M的弧长正好等于v的长度|v|,则定义

  .引理1 对于曲面M上的每点p0，存在包含p0的一个坐标邻域U及常数

，使得对于每点

和p点切空间T(M)中每个长度小于ε的切向量v，都有唯一的一条满足初始条件

的测地线:

设

，若存在测地线

满足初始条件

那么点

叫做在q点切向量v的指数映像，用

表示γ(1)，而映射

称为在q点的指数映射．于是，满足初始条件的唯一测地线可表达为

根据引理1 当||v|| 充分小时，

是确定的．一般地说，对于长度较长的向量v，指数映像

未必能确定．然而如果能确定，则总是唯一的．

定义 若对于任何点

和任何向量

，指数映像

总是确定的，则曲面M称为测地完备的．

显然，测地完备性等价于下述要求：对于每段测地线段

，总能够把

延拓成无限长的测地线：

因此，我们也可把后者作为测地完备性的定义   ．

与李代数

研究李代数元素的另一种方法是把它看作群上的左不变向量场．迄今为止，我们只是讨论单位元处的向量，对于向量场，需要涉及所有群元素的切线．将一个群元素在左侧相乘。就定义了群流形的一个同构

，其中

，群在它的基础流形上的这个作用诱导出在该流形向量场上的作用．左不变向量场关于这个作用是固定不变的．将任何左不变向量场限制到单位元上的切向量。即一个李代数元素．而给出一个单位元上的切向量。就能产生一个左不变向量场．我们需要做的就是左平移原始向量到流形上的每个点．如果X是一个矩阵。描述单位元处的切向量。则在群的点g处的切向量定义为gX．因此，单位元的切向量和左不变向量场之间是一一对应的．

这些左不变向量场的积分曲线在后面起重要的作用．向量场的积分曲线是在每一点都与该场相切的曲线．对于左不变向量场。这个曲线满足如下微分方程：

这个方程有解析解，通过单位元素的解是

矩阵X的指数可以展开成幂级数：

对于矩阵指数有如下关系：

当且仅当

．

这表示只有当指数是可交换时，指数积运算时指数才可以相加．当然，元素

和

是可交换的，这表示形如

的群元素构成子群：

它们是群的一维或单参数子群．用这种方法。每个李代数元素都产生一个单参数子群．

指数函数也可以被看作给出了从李代数到群的映射。这个映射通常既不是单射也不是满射，但是在单位元附近它是同胚映射．即在李代数上存在0的邻域同胚映射到群的单位元的邻域．在这个邻域存在一个逆映射。通常被称作对数，由众所周知的Mercator级数定义。即

当g远离单位元时，级数不收敛．

矩阵指数的行列式是矩阵迹的指数：

矩阵的迹Tr()是它的对角线元素之和．如果矩阵X的特征值都不相同。那么这个关系能够通过对角化矩阵简单地证明．即使在一般情况下，这个关系也是正确的．由这个关系可以得到：矩阵指数的行列式为1当且仅当矩阵是迹为0的．这就是李代数so(n),su(n)和sl(n)由迹为0的矩阵构成的原因．

对于某些李代数，我们能够更详细地确定它的指数映射．例如。考虑su(2),典型的李代数元素m用伴随表示可以描述成如下形式的矩阵：

通过简单的计算可以得到

．如果要求

。则得到

．由此将

看作是参数t²。将它们代入到指数定义得到

这也可以用原始的李代数元素

M

写作

可以由M的行列式得到t．

上述关系是线性的。这意味着对数也能够简单地求出．如果U是su(2)的元素。则

这里,t可以根据等式

得到．如上所述，这个对数并不是在整个群上有定义，显然上面得到的公式在

弧度时无意义   ．