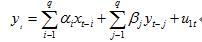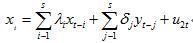格兰杰因果关系检验（克莱夫·格兰杰开创的检验方法）

背景

格兰杰本人在其2003年获奖演说中强调了其引用的局限性，以及“很多荒谬论文的出现”（Of course, many ridiculous papers appeared）。由于其统计学本质上是对平稳时间序列数据一种预测，仅适用于计量经济学的变量预测，不能作为检验真正因果性的判据。

在时间序列情形下，两个经济变量X、Y之间的格兰杰因果关系定义为：若在包含了变量X、Y的过去信息的条件下，对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果，即变量X有助于解释变量Y的将来变化，则认为变量X是引致变量Y的格兰杰原因。

进行格兰杰因果关系检验的一个前提条件是时间序列必须具有平稳性，否则可能会出现虚假回归问题。因此在进行格兰杰因果关系检验之前首先应对各指标时间序列的平稳性进行单位根检验(unit root test)。常用增广的迪基—富勒检验(ADF检验)来分别对各指标序列的平稳性进行单位根检验。

公式介绍

格兰杰因果关系检验假设了有关y和x每一变量的预测的信息全部包含在这些变量的时间序列之中。检验要求估计以下的回归：

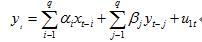
格兰杰因果关系检验

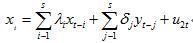
格兰杰因果关系检验

其中白噪音u1t 和u2t假定为不相关的。

式（1）假定当前y与y自身以及x的过去值有关，而式（2）对x也假定了类似的行为。

对式（1）而言，其零假设H0 ：α1=α2=…=αq=0。

对式（2）而言，其零假设H0 ：δ1=δ2=…=δs=0。

分四种情形讨论：

（1）x是引起y变化的原因，即存在由x到y的单向因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显著不为零，同时式（2）中滞后的y的系数估计值在统计上整体的显著为零，则称x是引起y变化的原因。

（2）y是引起x变化的原因，即存在由y到x的单向因果关系。若式（2）中滞后的y的系数估计值在统计上整体的显著不为零，同时式（1）中滞后的x的系数估计值在统计上整体的显著为零，则称y是引起x变化的原因。

（3）x和y互为因果关系，即存在由x到y的单向因果关系，同时也存在由y到x的单向因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显著不为零，同时式（2）中滞后的y的系数估计值在统计上整体的显著不为零，则称x和y间存在反馈关系，或者双向因果关系。

（4）x和y是独立的，或x与y间不存在因果关系。若式（1）中滞后的x的系数估计值在统计上整体的显著为零，同时式（2）中滞后的y的系数估计值在统计上整体的显著为零，则称x和y间不存在因果关系。

三、格兰杰因果关系检验的步骤

（1）将当前的y对所有的滞后项y以及别的什么变量（如果有的话）做回归，即y对y的滞后项yt-1，yt-2，…，yt-q及其他变量的回归，但在这一回归中没有把滞后项x包括进来，这是一个受约束的回归。然后从此回归得到受约束的残差平方和RSSR。

（2）做一个含有滞后项x的回归，即在前面的回归式中加进滞后项x，这是一个无约束的回归，由此回归得到无约束的残差平方和RSSUR。

（3）零假设是H0：α1=α2=…=αq=0，即滞后项x不属于此回归。

（4）为了检验此假设，用F检验，即：

它遵循自由度为q和(n-k)的F分布。在这里，n是样本容量，q等于滞后项x的个数，即有约束回归方程中待估参数的个数，k是无约束回归中待估参数的个数。

（5）如果在选定的显著性水平α上计算的F值超过临界值Fα，则拒绝零假设，这样滞后x项就属于此回归，表明x是y的原因。

（6）同样，为了检验y是否是x的原因，可将变量y与x相互替换，重复步骤（1）～（5）。

格兰杰因果关系检验对于滞后期长度的选择有时很敏感。其原因可能是被检验变量的平稳性的影响，或是样本容量的长度的影响。不同的滞后期可能会得到完全不同 的检验结果。因此，一般而言，常进行不同滞后期长度的检验，以检验模型中随机干扰项不存在序列相关的滞后期长度来选取滞后期。

格兰杰检验的特点决定了它只能适用于时间序列数据模型的检验，无法检验只有横截面数据时变量间的关系。

可以看出，我们所使用的Granger因果检验与其最初的定义已经偏离甚远，削减了很多条件（并且由回归分析方法和F检验的使用我们可以知道还增强了若干 条件），这很可能会导致虚假的格兰杰因果关系。因此，在使用这种方法时，务必检查前提条件，使其尽量能够满足。此外，统计方法并非万能的，评判一个对象，往往需 要多种角度的观察。正所谓“兼听则明，偏听则暗”。诚然真相永远只有一个，但是也要靠科学的探索方法。

值得注意的是，格兰杰因果关系检验的结论只是一种预测，是统计意义上的“格兰杰因果性“，而不是真正意义上的因果关系，不能作为肯定或否定因果关系的根据。当然，即使格兰杰因果关系不等于实际因果关系，也并不妨碍其参考价值。因为在经济学中，统计意义上的格兰杰因果关系也是有意义的，对于经济预测等仍然能起一些作用。

由于假设检验的零假设是不存在因果关系，在该假设下F统计量服从F分布，因此严格地说，该检验应该称为格兰杰非因果关系检验。