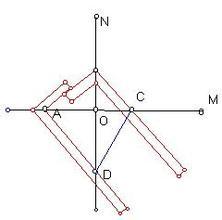
倍立方问题,是指作一个立方体,使它的体积是已知立方体的体积的两倍;化圆为方问题:作一个正方形,使它的面积等于已知圆的面积。在2400年前的古希腊已提出这些问题,直至1837年,法国数学家万芝尔才首先证明“三等分角”和“倍立方”为尺规作图不能问题。1882年德国数学家林德曼证明π是超越数后,“化圆为方”也被证明为尺规作图不能问题。
精选百科
本文由作者推荐
倍立方问题相关的文章
电影《被嫌弃的松子的一生》(日语:嫌われ松子の一生)改编自山田宗树所著同名小说,由中岛哲也编剧、导演,石田雄治、佐谷秀美、间濑泰宏、小玉圭太等主演,于2006年5月27日在日本首映。
陆无双,金庸小说《神雕侠侣》中的人物。原是江南陆家庄的千金小姐,陆家庄二庄主陆立鼎的女儿,幼时遭“赤练仙子”李莫愁灭门,并被其掳去,后成为李莫愁的徒弟,长大后偶遇杨过,并对杨过暗暗倾心。
成宫宽贵(Hiroshige Narimiya,1982年9月14日出生于东京都新宿区),日本影视男演员,曾是Top Coat事务所旗下艺人。2000年,成宫宽贵通过参演话剧《残存人类、爱之本质》正式出道。2002年,他凭借“J-PHONE”广告和与校园剧《极道鲜师》的表现受到大众关注。2004年,
西罗马帝国是罗马帝国在286年被戴克里先分为两部分后建立的四帝共治制的产物。395年,最后一位统一罗马帝国的皇帝狄奥多西一世驾崩,将罗马帝国分给两个儿子分别继承,从此罗马帝国正式分裂为东西罗马帝国。西罗马帝国的正式名称与东罗马帝国相同,均用罗马共和时代的国名“元老院与罗马人民”。在410年,西哥特人
高僧高僧:宋代文物陶模高僧宋代(960年—1279年)开封基本信息出土地点东京所属年代宋代基本信息【藏品名称】:高僧【藏品现状】:开封大学大观博物馆收藏藏品介绍高僧宋代(960年—1279年)开封HierarchSongDynasty(960–1279A.D.

尚可名片
这家伙太懒了,什么都没写!
作者