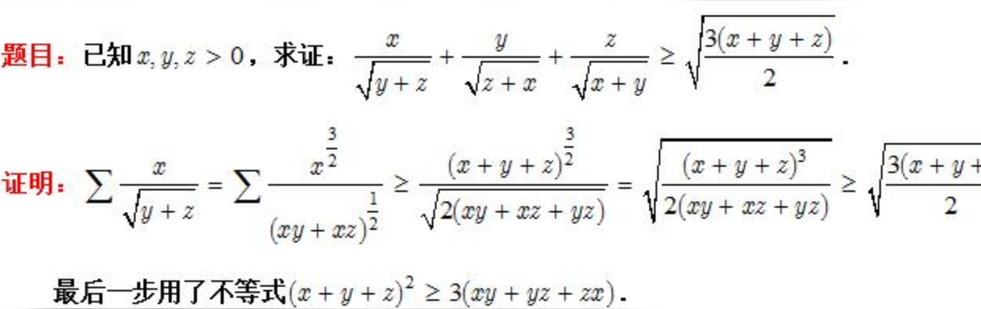权方和不等式（用于放缩求最值等的不等式）

公式简介

权方和不等式

是一个数学中重要的不等式。

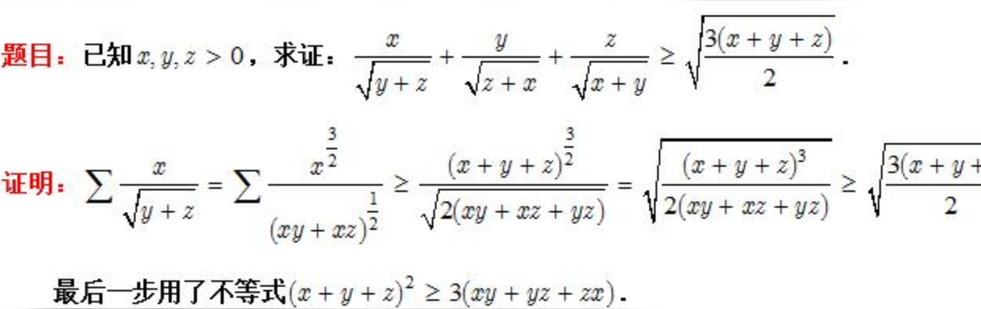
权方和不等式

形式

对于xi，yi>0，当m(m+1）>0时：

(x+x+x+………+x+……+x)/(y+y+y+…………+y+……+y)

≤

m(m+1）=0时：

(x+x+x+………+x+……+x)/(y+y+y+…………+y+……+y)

=

m(m+1）<0时：

(x+x+x+………+x+……+x)/(y+y+y+…………+y+……+y)

≥

其中n是正整数。

取等号的条件：x/y=x/y=x/y=…………=x/y=……=x/y.

证明

其证明需要用到

赫尔德（Holder）不等式

（特殊情形）

对于实数p和q，若p≥1，q<+∞，且1/p+1/q=1.

则对于所有实数或复数a1,a2,a3…………ai……an和b1,b2,b3…………bi……bn

恒有|a1b1|+|a2b2|+|a3b3|+……+|aibi|+……+|anbn|≤

[(|a1|^p+|a2|^p+|a3|^p+……+|ai|^p+……+|an|^p)^（1/p)]*

[(|b1|^q+|b2|^q+|b3|^q+…+|bi|^q+……+|bn|^q)^（1/q)]

当且仅当a1^p/b1^q=a2^p/b2^q=a3^p/b3^q=………=ai^p/bi^q=……=an^p/bn^q时，等号成立。

：因为m(m+1）>0，所以m>0或m<-1.

设ai=xi/yi^[m/(m+1）] bi=yi^[m/(m+1）]

p=m+1 q=(m+1）/m

m>0时，p>1，q<+∞成立，且1/p+1/q=1.

所以对于ai、bi>0，恒有：

|a1b1|+|a2b2|+|a3b3|+………+|aibi|+…+|anbn|≤

[(|a1|^p+|a2|^p+|a3|^p+……..……+|ai|^p+……+|an|^p)^（1/p)]*

[(|b1|^q+|b2|^q+|b3|^q+……....……+|bi|^q+……+|bn|^q)^（1/q)]

也就是x1+x2+x3+…………+xi+……+xn≤{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+

[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}^[1/(m+1）]

*{(y1+y2+y3+…………+yi+……+yn)^[m/(m+1）]}

不等式两边同时取（m+1）次幂，得到：

（x1+x2+x3+…………+xi+……+xn)^(m+1）≤{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+

[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}*

（y1+y2+y3+…………+yi+……+yn)^m

不等式两边同除（y1+y2+y3+…………+yi+……+yn)^m，就得到

（x1+x2+x3+……+xi+……+xn)^(m+1）/(y1+y2+y3+…………+yi+……+yn)^m≤{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}.得证.

另设ai=yi/xi^[(m+1）/m],bi=xi^[(m+1）/m]

p=-m q=m/(m+1）

当m1，q<+∞成立，且1/p+1/q=1.

所以对于ai、bi>0，恒有：

|a1b1|+|a2b2|+|a3b3|+…………+|aibi|+……+|anbn|≤

[(|a1|^p+|a2|^p+|a3|^p+…………+|ai|^p+……+|an|^p)^（1/p)]*

[(|b1|^q+|b2|^q+|b3|^q+…………+|bi|^q+……+|bn|^q)^（1/q)].

也就是y1+y2+y3+…………+yi+……+yn≤（x1+x2+x3+…………+xi+……+xn)^[(m+1）/m]

*{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}^(-1/m).

不等式两边同时做m次幂，此时不等号方向改变：

（y1+y2+y3+…………+yi+……+yn)^m≥（x1+x2+x3+…………+xi+……+xn)^(m+1）

*{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}^(-1）

不等式两边取倒数（不等号方向改变）再同乘（x1+x2+x3+…………+xi+……+xn)^(m+1），即得：

（x1+x2+x3+………+xi+……+xn)^(m+1）/(y1+y2+y3+…………+yi+……+yn)^m≤{[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]}.

第一式得证。

m就-1和0两种取值。

m=0时，原式简化为x1+x2+x3+…………+xi+……+xn=x1+x2+x3+…………+xi+……+xn显然成立；

m=-1时，原式简化为y1+y2+y3+…………+yi+……+yn=y1+y2+y3+…………+yi+……yn显然成立.

第二式得证。

设ai=yi^(-m),bi=xi^(m+1）.

p=-1/m,q=1/(m+1）.

当m(m+1）m>-1.

此时p>1，q<+∞成立，且1/p+1/q=1.

也就是[x1^(m+1）/y1^m]+[x2^(m+1）/y2^m]+[x3^(m+1）/y3^m]+…………+[xi^(m+1）/yi^m]+……+[xn^(m+1）/yn^m]≤[(x1+x2+x3+…………+xi+……+xn)^(m+1）]/[(y1+y2+y3+…………+yi+……+yn)^m].

第三式得证。

证毕.

赫尔德不等式取等号的条件是：

当且仅当a1^p/b1^q=a2^p/b2^q=a3^p/b3^q=…………=ai^p/bi^q=……=an^p/bn^q时等号成立。

所以第一式中，取等号的条件分别是：

m>0时候：

x1^(m+1）/y1^(m+1）=x2^(m+1）/y2^(m+1）=x3^(m+1）/y3^(m+1）=…………=

xi^(m+1）/yi^(m+1）=……=xn^(m+1）/yn^(m+1）.

m<-1时候：

x1^m/y1^m=x2^m/y2^m=x3^m/y3^m=…………=xi^m/yi^m=……=xn^m/yn^m.

第三式中，取等号的条件是：

0>m>-1时候：

y1/x1=y2/x2=y3/x3=…………=yi/xi=……=yn/xn.

由于xi、yi都是正数（也正因为这样，利用赫尔德不等式证明权方和不等式时才能把绝对值符号去掉），所以可以分别通过开（m+1）、m、-1次方简化为：

x1/y1=x2/y2=x3/y3=…………=xi/yi=……=xn/yn时等号成立。

其他信息

权方和不等式是在高中竞赛中很有用的一个不等式，常用来处理分式不等式。

它和赫尔德不等式的这个特殊情形是等价关系。

其中m称为不等式的权，特点是分子次数比分母高一次。

可用于处理分式不等式、放缩求最值（极值）、证明不等式等方面，对高中数学竞赛有帮助。