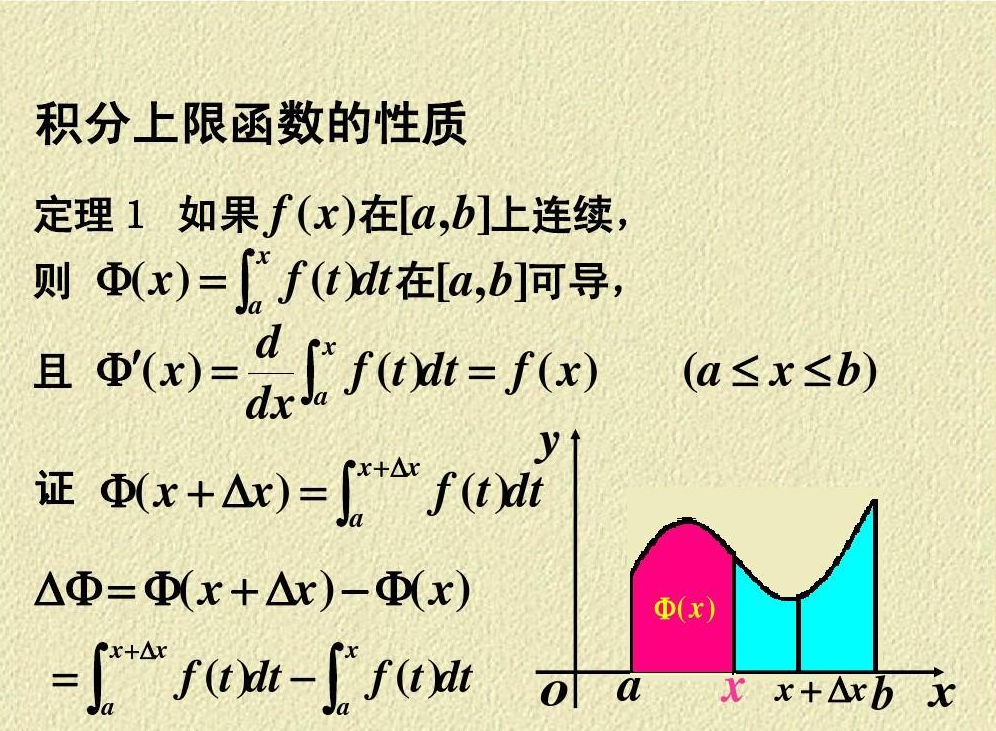
设函数y=f(x)在区间[a,b]上可积,对任意x∈[a,b],y=f(x)在[a,x]上可积,且它的值与x构成一种对应关系(如概述中的图片所示),称Φ(x)为变上限的定积分函数,简称积分上限函数。
积分上限函数相关的文章
有机化合物一般是指含碳氢键的化合物,因此不包括碳氧化物(如一氧化碳、二氧化碳)、碳酸盐、氰化物、硫氰化物、氰酸盐、金属碳化物等物质。但是,部分不包含碳氢键的化合物,如四氯化碳等全卤代烃,可以看作氢原子被卤素取代的产物,仍属于有机化合物。
玉山铁二(1980年4月7日出生于日本京都府城阳市)是一位日本影视男演员。他毕业于京都府立西城阳高中,并于1999年通过出演个人首部电视剧《麻辣女教师》正式进入演艺圈。2001年,他参演了特摄剧《百兽战队牙吠联者》。2004年,玉山铁二首次担任主演,出演运动电影《功夫棒球》,在片中饰演不屈斗志。20
鼻炎是一种常见的鼻腔黏膜炎症性疾病。多发生于春夏交替的季节,我国发病率呈上升的趋势。病因较为复杂,与多种因素有关,病毒感染是首要原因。主要表现为鼻塞、鼻痒、打喷嚏、流鼻涕、嗅觉下降、头痛、头昏等。主要通过药物治疗来缓解症状,此外还会有变应原特异性免疫治疗、手术治疗等。如未及时治疗,可能会引起急性鼻窦
撒丁岛(Sardegna)是地中海意大利仅次于西西里岛的第二大岛屿,面积2.4090万平方公里,人口约165.6万人。岛上有平原和花岗岩山地,海滩风光绚丽,地中海气候。北距法国的科西嘉岛12公里,南距非洲海岸200公里。首府卡利亚里(Cagliari)。
阿尔泰山脉(英语:Altai Mountains;俄语:Алтай),是位于欧亚大陆中部的山系,坐落在北纬45°~52°,东经84°~99°之间,地跨哈萨克斯坦、俄罗斯、中国和蒙古四国,整体呈西北-东南走向。其东北与萨彦岭相连,随后地势向东南逐渐变低,并与戈壁沙漠相接。该山脉东西总长约2000千米,
乌鲁却勒镇位于阿瓦提县城东南18公里,东与阔如勒墩农场相连,南以巴楚、墨玉、洛浦等县相接,西与阿依巴克乡接壤,北邻恒丰公司和阿瓦提镇,东西宽20公里,南北长37.2公里,总面积744平方公里。

尚可名片
这家伙太懒了,什么都没写!