精选百科
本文由作者推荐
红外光谱分析
对物质分子进行的分析、鉴定
红外光谱分析（infrared spectra analysis指的是利用红外光谱对物质分子进行的分析和鉴定。将一束不同波长的红外射线照射到物质的分子上，某些特定波长的红外射线被吸收，形成这一分子的红外吸收光谱。
基本信息
| 中文名 | 红外光谱分析 |
| 外文名 | infrared spectra analysis |
| 类型 | 物理学名词 |
| 所属学科 | 物理学 |
| 用途 | 对物质分子进行的分析和鉴定 |
工作原理
每种分子都有由其组成和结构决定的独有的红外吸收光谱，据此可以对分子进行结构分析和鉴定。红外吸收光谱是由分子不停地作振动和转动运动而产生的，分子振动是指分子中各原子在平衡位置附近作相对运动，多原子分子可组成多种振动图形。当分子中各原子以同一频率、同一相位在平衡位置附近作简谐振动时，这种振动方式称简正振动（例如伸缩振动和变角振动）。分子振动的能量与红外射线的光量子能量正好对应，因此当分子的振动状态改变时，就可以发射红外光谱，也可以因红外辐射激发分子而振动而产生红外吸收光谱。分子的振动和转动的能量不是连续而是量子化的。但由于在分子的振动跃迁过程中也常常伴随转动跃迁，使振动光谱呈带状。所以分子的红外光谱属带状光谱。
基本种类
主要用途
解析方法
常用术语
其它介绍
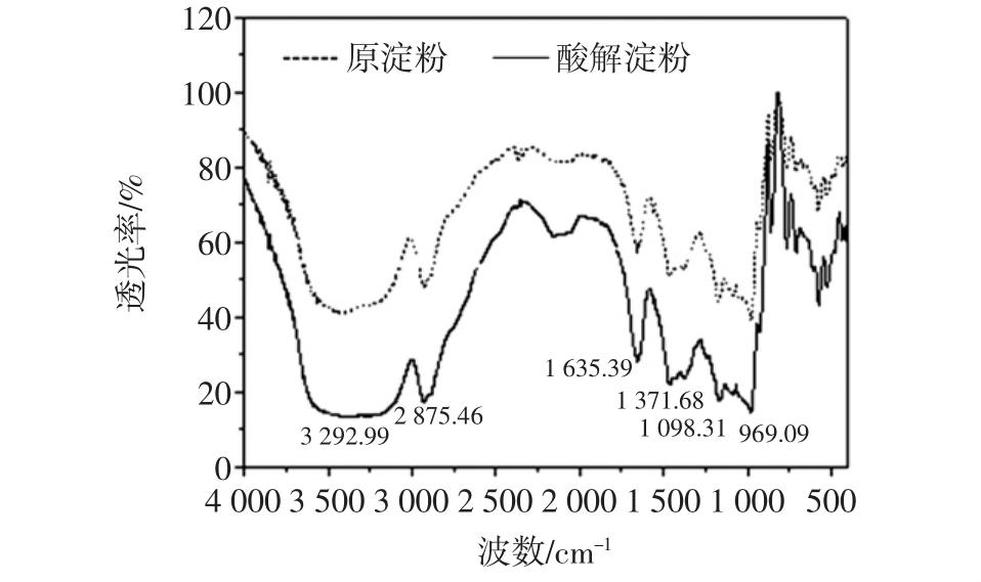
红外吸收与振动 - 转动光谱
1. 光谱的产生：
分子中基团的振动和转动能级跃迁产生振-转光谱，称红外光谱。
2. 所需能量：
近红外（
），中红外（
），远红外（
）
3. 研究对象：
具有红外活性的化合物，即含有共价键、并在振动过程中伴随有偶极矩变化的化合物。
4. 用途：
结构鉴定、定量分析和化学动力学研究等。
分子振动方程式
1. 振动频率
2.振动能级（量子化）：
任意两个相邻的能级间的能量差为：
（用波数表示）
发生振动能级跃迁需要能量的大小取决于键两端原子的折合质量和键的力常数，即取决于分子的结构特征。
化学键键强越强（即键的力常数 K 越大）原子折合质量越小，化学键的振动频率越大，吸收峰将出现在高波数区。
键类型
力常数
峰位 4.5mm 6.0mm 7.0mm
分子的振动形式
红外光谱产生的条件
1. 红外光的频率与分子中某基团振动频率一致；
2. 分子振动引起瞬间偶极矩变化
偶极子在交变电场中的作用示意图
红外光谱峰的位置、峰数与强度
1.位置：
由振动频率决定，化学键的力常数 K 越大，原子折合质量 m 越小，键的振动频率越大，吸收峰将出现在高波数区（短波长区）；反之，出现在低波数区（高波长区）；
2.峰数：
非线性分子：
线性分子：
绝大多数化合物红外吸收峰数远小于理论计算振动自由度，其原因有：无偶极矩变化的振动不产生红外吸收；吸收简并；吸收落在仪器检测范围以外；仪器分辨率低，谱峰重叠等。
3．强度：
红外吸收的强度与 跃迁几率的大小和振动偶极矩变化的大小有关，跃迁几率越大、振动偶极矩越大，则吸收强度越大。
4 ．红外光谱图：
纵坐标为吸收强度，横坐标为波长 λ ， （ μ m ），和波数
，单位：
，可以用峰数，峰位，峰形，峰强来描述
红外光谱分析相关的文章
风热，是病证名，风和热相结合的病邪，临床表现为发热重、恶寒较轻、咳嗽、口渴、舌边尖红、苔微黄、脉浮数，甚则口燥、目赤、咽痛、衄血等。是风热之邪犯表、肺气失和所致。治以疏风清热为主。
阿拉伯（阿拉伯语：العربية），可指阿拉伯民族，也可指阿拉伯世界。阿拉伯民族起源于闪米特种族，是闪族最年轻的一支，亲缘上与希伯来人相近。阿拉伯世界泛指阿拉伯人居住的地区，阿拉伯世界共有22个国家和地区。
准噶尔盆地（英文Junggar Basin；“噶”为gá），位于中国新疆的北部，是中国第二大的内陆盆地。准噶尔盆地位于阿尔泰山与天山之间，西侧为准噶尔西部山地，东至北塔山麓。盆地呈不规则三角形，地势向西倾斜，北部略高于南部，北部的乌伦古湖（布伦托海）湖面高程479.1米，中部的玛纳斯湖湖面270米，
尚可名片
这家伙太懒了，什么都没写！
作者
